如图,在等腰梯形ABCD中,AB∥DC,AB=8cm,CD=2cm,AD=6cm。点P从点A出发,以2cm/s的速度沿AB向终点B运动;点Q从点C出发,以1cm/s的速度沿CD、DA向终点A运动(P、Q两点中,有一个点运动到终点时,所有运动即终止).设P、Q同时出发并运动了t秒。
(1)当PQ将梯形ABCD分成两个直角梯形时,求t的值;
(2)试问是否存在这样的t,使四边形PBCQ的面积是梯形ABCD面积的一半?若存在,求出这样的t的值,若不存在,请说明理由。
相关知识点
推荐套卷
 )
)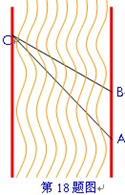
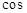 В是关于x的方程kx2-kx+1=0的两个根,求∠B的度数. (11分)
В是关于x的方程kx2-kx+1=0的两个根,求∠B的度数. (11分)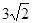 ,ad⊥bc于d,求cd
,ad⊥bc于d,求cd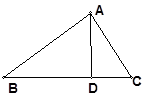
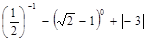 +
+ 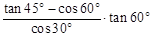
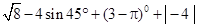
 秒)表示移动时间,当这两点中有一点到达自己的终点时,另一点也停止运动。
秒)表示移动时间,当这两点中有一点到达自己的终点时,另一点也停止运动。 粤公网安备 44130202000953号
粤公网安备 44130202000953号