初中数学圆填空题

如图， $\angle \mathit{MON}=40°$ ，以 $O$ 为圆心，4为半径作弧交 $\mathit{OM}$ 于点 $A$ ，交 $\mathit{ON}$ 于点 $B$ ，分别以点 $A$ ， $B$ 为圆心，大于 $\frac{1}{2}\mathit{AB}$ 的长为半径画弧，两弧在 $\angle \mathit{MON}$ 的内部相交于点 $C$ ，画射线 $\mathit{OC}$ 交 $\stackrel{̂}{\mathit{AB}}$ 于点 $D$ ， $E$ 为 $\mathit{OA}$ 上一动点，连接 $\mathit{BE}$ ， $\mathit{DE}$ ，则阴影部分周长的最小值为 　　．

如图1，正方形纸片ABCD的边长为2，翻折∠B、∠D，使得两个直角的顶点重合于对角线BD上一点P，EF、GH分别是折痕（如图2）．设AE＝x（0＜x＜2），给出下列判断：

①当x＝1时，点P是正方形ABCD的中心；
②当x＝时，EF＋GH＞AC；
③当0＜x＜2时，六边形AEFCHG面积的最大值是；
④当0＜x＜2时，六边形AEFCHG周长的值不变．
其中正确的是________（填序号）．

 已知正方形ABCD的边长AB=k（k是正整数），等边三角形PAE的顶点P在正方形内，顶点E在边AB上，且AE="1." 将等边三角形PAE在正方形内按图中所示的方式，沿着正方形的边AB、BC、CD、DA、AB、…连续地翻转n次，使顶点P第一次回到原来的起始位置. ①如果k=1，那么顶点P第一次回到原来的起始位置时，△PAE沿正方形的边连续翻转的次数n=       ；②如果顶点P第一次回到原来的起始位置时，等边三角形PAE沿正方形的边连续翻转的次数是84，那么正方形ABCD的边长k=         .

若从矩形一边上的点到对边的视角是直角，即称该点是直角点。例如，如图的矩形中，点在边上，连接，,则点为直角点。若点分别为矩形的边上的直角点，且,,则的长为     

如图，正方形ABCD的边长为2，AE＝EB，MN＝1，线段MN的两端在CB、CD上滑动，当CM＝      时，△AED与以M、N、C为顶点的三角形相似。

如图，有一块边长为4的正方形塑料摸板ABCD，将一块足够大的直角三角板的直角顶点落在A点，两条直角边分别与CD交于点F，与CB延长线交于点E．则四边形AECF的面积是 ▲   .

在菱形ABCD中，∠ABC=60°，边长为2cm，E,F分别是边BC和对角线BD上两个动点，则EF＋CF的最小值为___________________________.

如图（2），正方形ABCD的面积为18，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一动点P，则PD + PE的最小值为                 .

如图所示，直线与y轴交于点，以为边作正方形然后延长与直线交于点，得到第一个梯形；再以为边作正方形，同样延长与直线交于点得到第二个梯形；，再以为边作正方形，延长，得到第三个梯形；……则第2个
的面积是          ；第（n是正整数）个梯形的面积是           （用含n的式子
表示）．

如图平行四边形ABCD中AB=AD=6，∠DAB=60度，F为AC上一点，E为AB中点，则EF+BF的最小值为        ．

请同学们认真阅读、研究，完成“类比猜想”及后面的问题．
习题解答：
习题如图13（1），点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则EF=BE+DF，说明理由．
解答：∵正方形ABCD中，AB=AD，∠BAD=∠ADC=∠B=90°，
∴把△ABE绕点A逆时针旋转90°至△ADE′，点F、D、E′在一条直线上．
∴∠E′AF=90°﹣45°=45°=∠EAF，
又∵AE′=AE，AF=AF
∴△AE′F≌△AEF（SAS）
∴EF=E′F=DE′+DF=BE+DF．
习题研究
观察分析：观察图（1），由解答可知，该题有用的条件是①ABCD是四边形，点E、F分别在边BC、CD上；②AB=AD；③∠B=∠D=90°；④∠EAF=∠BAD．
类比猜想：（1）在四边形ABCD中，点E、F分别在BC、CD上，当AB=AD，∠B=∠D时，还有EF=BE+DF吗？
研究一个问题，常从特例入手，请同学们研究：如图13（2），在菱形ABCD中，点E、F分别在BC、CD上，当∠BAD=120°，∠EAF=60°时，还有EF=BE+DF吗？
（2）在四边形ABCD中，点E、F分别在BC、CD上，当AB=AD，∠B+∠D=180°，∠EAF=∠BAD时，EF=BE+DF吗？
归纳概括：反思前面的解答，思考每个条件的作用，可以得到一个结论“EF=BE+DF”的一般命题：       ．

如图，在菱形ABCD中，AB=6，∠ABC=60°，点E在AD上，且AE=2，点P是对角线BD上的一个动点，则PE+PA的最小值是                    ．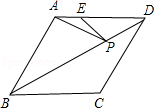

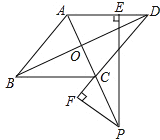
如图，在菱形ABCD中，对角线AC、BD相交于点O，AC=6，BD=8，点P是AC延长线上的一个动点，过点P作PE⊥AD，垂足为E，作CD延长线的垂线，垂足为E，则|PE-PF|=   ．

如图，在矩形ABCD中，AB=16，BC=12，顺次连结各边中点，得菱形;再顺次连结菱形的各边中点，得矩形；再顺次连结矩形的各边中点，得菱形，……这样继续下去．则图中的四边形的周长等于        ，图中的四边形的面积等于           ．

图1是邻边长为2和6的矩形，它由三个小正方形组成，将其剪拼成不重叠、无缝隙的大正方形（如图 $2)$ ，则图1中所标注的 $d$ 的值为 　　；记图1中小正方形的中心为点 $A$ ， $B$ ， $C$ ，图2中的对应点为点 $A\text{'}$ ， $B\text{'}$ ， $C\text{'}$ ．以大正方形的中心 $O$ 为圆心作圆，则当点 $A\text{'}$ ， $B\text{'}$ ， $C\text{'}$ 在圆内或圆上时，圆的最小面积为 　　．