初中数学圆填空题

在矩形中，如果，，那么     ．

如图，在菱形ABCD中，对角线AC，BD相交于点O，AC=12，BD=16，E为AD中点，点P在x轴上移动．若△POE为等腰三角形，请写出所有符合要求的点P的坐标                ．

如图，在边长为10的菱形ABCD中，对角线BD ="16." 点E是AB的中点，P、Q是BD上的动点，且始终保持PQ ="2." 则四边形AEPQ周长的最小值为_________．（结果保留根号）

如图，正方形ABCD的边长为4+2，点E在对角线BD上，且∠BAE=，EF⊥AB，垂足为点F，则EF的长是           

如图，正方形ABCD中，点E在边AB上，且BE=，AE=3BE，点P在线段AC上的运动，则PE+PB的最小值为             。

如图，菱形ABCD和菱形ECGF的边长分别为2和4, ∠A=120°．则阴影部分面积是       ．（结果保留根号）

将一张长方形纸片按照图示的方式进行折叠：①翻折纸片，使A与DC边的中点M重合，折痕为EF；②翻折纸片，使C落在ME上，点C的对应点为H，折痕为MG；③翻折纸片，使B落在ME上，点B的对应点恰与H重合，折痕为GE．

根据上述过程，长方形纸片的长宽之比=             ．

如图，菱形OABC的面积为3，顶点O的坐标为（0，0），顶点A的坐标为（3，0），顶点B在第一象限，边BC与y轴交于点D，点E在边OA上．将四边形ABDE沿直线DE翻折，使点A落在第四象限的点F处，且FE⊥EA．则直线OF的解析式为        。

如图在矩形ABCD中，AD=4,M是AD的中点，点E是线段AB上的一动点，连接EM并延长交CD的延长线于点F，G是线段BC上的一点，连接GE 、GF、GM ．若△EGF是等腰直角三角形，=90°，则AB=      

如图，菱形纸片ABCD中，∠A=60°，将纸片折叠，点A、D分别落在A′、D′处，且A′D′经过B，EF为折痕，当D′F⊥CD时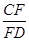，的值为    ．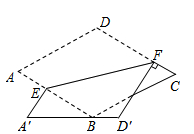

阅读探索：“任意给定一个矩形A，是否存在另一个矩形B，使它的周长和面积分别是已知矩形周长和面积的一半？”（完成下列空格）
（1）当已知矩形A的边长分别为6和1时，小亮同学是这样研究的：
设所求矩形的两边分别是，由题意得方程组：，
消去y化简得：，
∵△=49－48=1＞0，∴x₁=                ，x₂=                ．
∴满足要求的矩形B存在．
（2）如果已知矩形A的边长分别为2和1，请你仿照小亮的方法研究是否存在满足要求的矩形B．
（3）如果矩形A的边长为m和n，请你研究满足什么条件时，矩形B存在？

已知：如图，有长为24米的篱笆，一面利用墙（墙的最大可用长度a为10米），围成中间隔有一道篱笆的长方形花圃．设花圃的宽AB为x米，面积为S米²．则S与x的函数关系式            ；自变量的取值范围           ．

如图，在矩形ABCD中，AB=16，BC=12，顺次连结各边中点，得菱形;再顺次连结菱形的各边中点，得矩形；再顺次连结矩形的各边中点，得菱形，……这样继续下去．则图中的四边形的周长等于        ，图中的四边形的面积等于           ．

正方形、正方形和正方形的位置如图所示，点在线段上，已知
正方形的边长为3，则的面积为         ．

如图，平行四边形AOBC中，对角线交于点E，双曲线（k＞0）经过A，E两点，若平行四边形AOBC的面积为24，则k=　  　．