阅读探索:“任意给定一个矩形A,是否存在另一个矩形B,使它的周长和面积分别是已知矩形周长和面积的一半?”(完成下列空格)
(1)当已知矩形A的边长分别为6和1时,小亮同学是这样研究的:
设所求矩形的两边分别是 ,由题意得方程组:
,由题意得方程组: ,
,
消去y化简得: ,
,
∵△=49-48=1>0,∴x1= ,x2= .
∴满足要求的矩形B存在.
(2)如果已知矩形A的边长分别为2和1,请你仿照小亮的方法研究是否存在满足要求的矩形B.
(3)如果矩形A的边长为m和n,请你研究满足什么条件时,矩形B存在?
如图,正方形 的边长为2,以
的边长为2,以 为圆心、
为圆心、 为半径作弧
为半径作弧 交
交 于点
于点 ,设弧
,设弧 与边
与边 、
、 围成的阴影部分面积为
围成的阴影部分面积为 ;然后以
;然后以 为对角线作正方形
为对角线作正方形 ,又以
,又以 为圆心、
为圆心、 为半径作弧
为半径作弧 交
交 于点
于点 ,设弧
,设弧 与边
与边 、
、 围成的阴影部分面积为
围成的阴影部分面积为 ;…,按此规律继续作下去,设弧
;…,按此规律继续作下去,设弧 与边
与边 、
、 围成的阴影部分面积为
围成的阴影部分面积为 .则:(1)
.则:(1) = ;(2)
= ;(2) = .
= .
如图,菱形OABC的面积为3 ,顶点O的坐标为(0,0),顶点A的坐标为(3,0),顶点B在第一象限,边BC与y轴交于点D,点E在边OA上.将四边形ABDE沿直线DE翻折,使点A落在第四象限的点F处,且FE⊥EA.则直线OF的解析式为 。
,顶点O的坐标为(0,0),顶点A的坐标为(3,0),顶点B在第一象限,边BC与y轴交于点D,点E在边OA上.将四边形ABDE沿直线DE翻折,使点A落在第四象限的点F处,且FE⊥EA.则直线OF的解析式为 。
如图,在正方形ABCD内作一个等边三角形ABE,连接DE、CE,有如下结论:①图中除等边三角形ABE外,还有三个等腰三角形;②△ADE≌△BCE;③此图形既是中心对称图形也是轴对称图形;④△ABE的面积与正方形ABCD的面积比是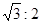 ;⑤△DEC与△ABE的面积比为
;⑤△DEC与△ABE的面积比为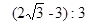 。则以上结论正确的是 .(只填正确结论的序号)
。则以上结论正确的是 .(只填正确结论的序号)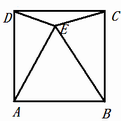
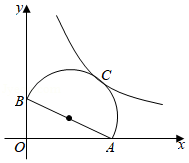
如图, 是半圆的直径, 为半圆的中点, , ,反比例函数 的图象经过点 ,则 的值为 .
如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:
①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+
其中正确的序号是______________
如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为6和8时,则阴影部分的面积为 .
已知菱形ABCD的两条对角线的长分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值= .
如图,在菱形ABCD中,对角线AC、BD相交于点O,AC=6,BD=8,点P是AC延长线上的一个动点,过点P作PE⊥AD,垂足为E,作CD延长线的垂线,垂足为E,则|PE-PF|= .
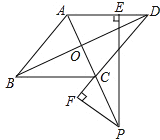
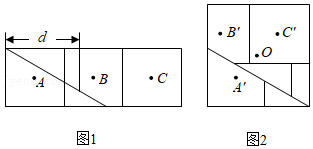
图1是邻边长为2和6的矩形,它由三个小正方形组成,将其剪拼成不重叠、无缝隙的大正方形(如图 ,则图1中所标注的 的值为 ;记图1中小正方形的中心为点 , , ,图2中的对应点为点 , , .以大正方形的中心 为圆心作圆,则当点 , , 在圆内或圆上时,圆的最小面积为 .
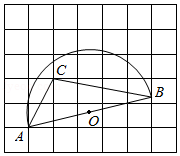
如图,在每个小正方形的边长为1的网格中, 的顶点 , 均落在格点上,点 在网格线上.
(Ⅰ)线段 的长等于 ;
(Ⅱ)以 为直径的半圆的圆心为 ,在线段 上有一点 ,满足 .请用无刻度的直尺,在如图所示的网格中,画出点 ,并简要说明点 的位置是如何找到的(不要求证明) .
如图, ,以 为圆心,4为半径作弧交 于点 ,交 于点 ,分别以点 , 为圆心,大于 的长为半径画弧,两弧在 的内部相交于点 ,画射线 交 于点 , 为 上一动点,连接 , ,则阴影部分周长的最小值为 .

如图,在矩形ABCD中,AB=16,BC=12,顺次连结各边中点,得菱形 ;再顺次连结菱形
;再顺次连结菱形 的各边中点,得矩形
的各边中点,得矩形 ;再顺次连结矩形
;再顺次连结矩形 的各边中点,得菱形
的各边中点,得菱形 ,……这样继续下去.则图中的四边形
,……这样继续下去.则图中的四边形 的周长等于 ,图中的四边形
的周长等于 ,图中的四边形 的面积等于 .
的面积等于 .

对正方形ABCD进行分割,如图1,其中E、F分别是BC、CD的中点,M、N、G分别是OB、OD、EF的中点,沿分化线可以剪出一副“七巧板”,用这些部件可以拼出很多图案,图2就是用其中6块拼出的“飞机”.若△GOM的面积为1,则“飞机”的面积为 .
如图,点P是正方形ABCD的对角线BD上的一个动点(不与B、D重合),连结AP,过点B作直线AP的垂线,垂足为H,连结DH,若正方形的边长为4,则线段DH长度的最小值是 .