如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为6和8时,则阴影部分的面积为 .
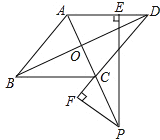
如图,在菱形ABCD中,对角线AC、BD相交于点O,AC=6,BD=8,点P是AC延长线上的一个动点,过点P作PE⊥AD,垂足为E,作CD延长线的垂线,垂足为E,则|PE-PF|= .
将一张长方形纸片按照图示的方式进行折叠:①翻折纸片,使A与DC边的中点M重合,折痕为EF;②翻折纸片,使C落在ME上,点C的对应点为H,折痕为MG;③翻折纸片,使B落在ME上,点B的对应点恰与H重合,折痕为GE.
根据上述过程,长方形纸片的长宽之比= .
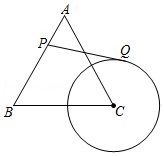
如图,等边三角形 的边长为4, 的半径为 , 为 边上一动点,过点 作 的切线 ,切点为 ,则 的最小值为 .
如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到点E时,小球P所经过的路程长为______________.
在平面直角坐标系 O
O 中,过原点O及点A(0,2) 、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D 点P从点O出发,以每秒
中,过原点O及点A(0,2) 、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D 点P从点O出发,以每秒 个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动 设移动时间为t秒,当t为 时,△PQB为直角三角形。
个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动 设移动时间为t秒,当t为 时,△PQB为直角三角形。
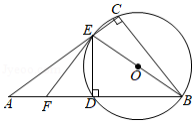
如图,在 中, , 的垂直平分线分别交 、 于点 、 , , 为 的外接圆,过点 作 的切线 交 于点 ,则下列结论正确的是 (写出所有正确结论的序号)
① ;
② ;
③若 ,则 的长为 ;
④ ;
⑤若 ,则 .
如图,在边长为10的菱形ABCD中,对角线BD ="16." 点E是AB的中点,P、Q是BD上的动点,且始终保持PQ ="2." 则四边形AEPQ周长的最小值为_________.(结果保留根号)
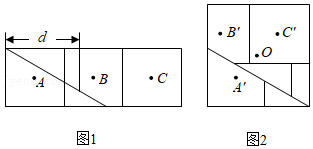
图1是邻边长为2和6的矩形,它由三个小正方形组成,将其剪拼成不重叠、无缝隙的大正方形(如图 ,则图1中所标注的 的值为 ;记图1中小正方形的中心为点 , , ,图2中的对应点为点 , , .以大正方形的中心 为圆心作圆,则当点 , , 在圆内或圆上时,圆的最小面积为 .
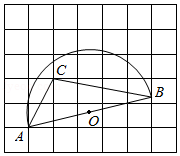
如图,在每个小正方形的边长为1的网格中, 的顶点 , 均落在格点上,点 在网格线上.
(Ⅰ)线段 的长等于 ;
(Ⅱ)以 为直径的半圆的圆心为 ,在线段 上有一点 ,满足 .请用无刻度的直尺,在如图所示的网格中,画出点 ,并简要说明点 的位置是如何找到的(不要求证明) .
如图, ,以 为圆心,4为半径作弧交 于点 ,交 于点 ,分别以点 , 为圆心,大于 的长为半径画弧,两弧在 的内部相交于点 ,画射线 交 于点 , 为 上一动点,连接 , ,则阴影部分周长的最小值为 .

如图,在矩形ABCD中,AB=16,BC=12,顺次连结各边中点,得菱形 ;再顺次连结菱形
;再顺次连结菱形 的各边中点,得矩形
的各边中点,得矩形 ;再顺次连结矩形
;再顺次连结矩形 的各边中点,得菱形
的各边中点,得菱形 ,……这样继续下去.则图中的四边形
,……这样继续下去.则图中的四边形 的周长等于 ,图中的四边形
的周长等于 ,图中的四边形 的面积等于 .
的面积等于 .

对正方形ABCD进行分割,如图1,其中E、F分别是BC、CD的中点,M、N、G分别是OB、OD、EF的中点,沿分化线可以剪出一副“七巧板”,用这些部件可以拼出很多图案,图2就是用其中6块拼出的“飞机”.若△GOM的面积为1,则“飞机”的面积为 .