江苏省张家港市九年级5月网上阅卷适应性考试数学试卷
下列运算正确的是
| A.2x+3y=5xy | B.5x2·x3=5x5 | C.4x8÷2x2=2x4 | D.(-x3)2=x5 |
已知∠1与∠2互补,并且∠1比∠2的3倍还大20°,若设∠1=x°,∠2=y°,则x、y满足的方程组为
A.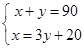 |
B.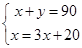 |
C.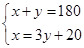 |
D.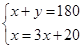 |
如图,在梯形ABCD中,AD∥BC,∠B=50°,∠C=80°,AE∥CD交BC于点E,若AD=2,BC=5,则边CD的长是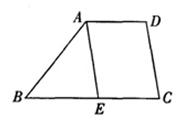
A.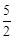 |
B. |
C.3 | D.4 |
反比例函数y=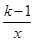 的图象如图所示,给出以下结论:①常数k<1;②在每一个象限内,y随x的增大而减小;③若点A(-l,a)和A'(l,b)都在该函数的图象上,则a+b=0;④若点B(-2,h)、C(
的图象如图所示,给出以下结论:①常数k<1;②在每一个象限内,y随x的增大而减小;③若点A(-l,a)和A'(l,b)都在该函数的图象上,则a+b=0;④若点B(-2,h)、C( ,m)、D(3,n)在该函数的图象上,则h<m<n,其中正确的结论是
,m)、D(3,n)在该函数的图象上,则h<m<n,其中正确的结论是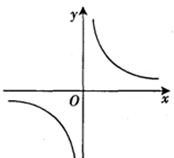
| A.①② | B.②③ | C.③④ | D.②④ |
如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于点E,且DE∥BC.已知AE=2 ,AC=3
,AC=3 ,BC=6,则⊙O的半径是
,BC=6,则⊙O的半径是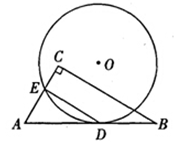
A.3 B.2 C.2
C.2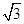 D.
D.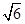
已知实数x,y满足x+y=-2a,xy=a(a≥1),则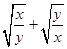 的值为
的值为
A.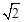 a a |
B.2a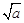 |
C.a |
D.2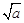 |
现有五张完全相同的卡片,上面分别写有“中国”、“美国”、“韩国”、“德国”、“英国”,把卡片背面朝上洗匀,然后从中随机抽取一张,抽到卡片对应的国家为亚洲的概率是
观察下列等式:
第1个等式:x1=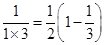 ;第2个等式:x2=
;第2个等式:x2=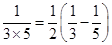 ;
;
第3个等式:x3=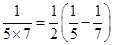 ;第4个等式:x4=
;第4个等式:x4=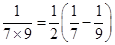 ;
;
则xl+x2+x3+…+x10= .
如图,点A在反比例函数y=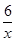 (x>0)图象上,且OA=4,过A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于B.则△ABC的周长为 .
(x>0)图象上,且OA=4,过A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于B.则△ABC的周长为 .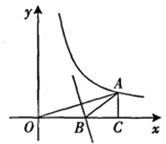
如图,已知半径为1的圆的圆心为M(0,1),点B(0,2),A是x轴负半轴上的一点,D是OA的中点,AB交⊙M于点C.若四边形BCDM为平行四边形,则sin∠ABD= .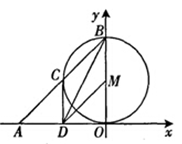
如图,点P是正方形ABCD的对角线BD上的一个动点(不与B、D重合),连结AP,过点B作直线AP的垂线,垂足为H,连结DH,若正方形的边长为4,则线段DH长度的最小值是 .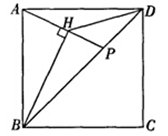
为了倡导“节约用水,从我做起”的活动,某市政府决定对市直机关500户家庭的用水情况作一次调查,调查小组随机抽查了其中100户家庭一年的月平均用水量(单位:吨).并将调查结果制成了如图所示的条形统计图.
(1)求这100个样本数据的平均数、众数和中位数;
(2)根据样本数据,估计该市直机关500户家庭中月平均用水量不超过12吨的约有多少户?
△ABC在平面直角坐标系xOy中的位置如图所示,点A的坐标为(-2,3),点B的坐标为(-1,1),点C的坐标为(0,2).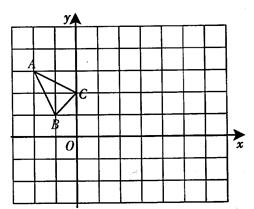
(1)作△ABC关于点C成中心对称的△A1BlCl.
(2)将△A1BlCl向右平移4个单位,作出平移后的△A2B2C2.
(3)点P是x轴上的一点,并且使得PA1+PC2的值最小,则点P的坐标为( , ).
为了决定谁将获得仅有的一张科普报告入场券,甲和乙设计了如下的摸球游戏:在不透明口袋中放入编号分别为1、2、3的三个红球及编号为4的一个白球,四个小球除了颜色和编号不同外,其它没有任何区别,摸球之前将袋内的小球搅匀,甲先摸两次,每次摸出一个球(第一次摸后不放回),把甲摸出的两个球放回口袋后,乙再摸,乙只摸一次且摸出一个球,如果甲摸出的两个球都是红色,甲得1分,否则,甲得0分,如果乙摸出的球是白色,乙得1分,否则乙得0分,得分高的获得入场券,如果得分相同,游戏重来.
(1)运用列表或画树状图求甲得1分的概率;
(2)请你用所学的知识说明这个游戏是否公平?
如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于点N,连接BM、DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求菱形BMDN的面积和对角线MN的长.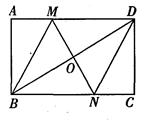
如图,在△ABC中,D是AB边上一点,⊙O过D、B、C三点,∠DOC=2∠ACD=90°.
(1)求证:直线AC是⊙O的切线;
(2)如果∠ACB=75°.
①若⊙O的半径为2,求BD的长;
②求CD:BC的值.
快、慢两车分别从相距360千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,快车到达乙地后,停留1小时,然后按原路原速返回,快车比慢车晚1小时到达甲地,快、慢两车距各自出发地的路程y(千米)与出发后所用的时间x(小时)的关系如图所示.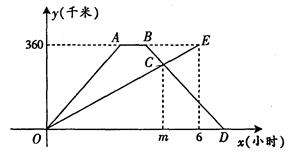
请结合图象信息解答下列问题:
(1)慢车的速度是 千米/小时,快车的速度是 千米/小时;
(2)求m的值,并指出点C的实际意义是什么?
(3)在快车按原路原速返回的过程中,快、慢两车相距的路程为150千米时,慢车行驶了多少小时?
在平面直角坐标系xOy中,一次函数y=-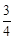 x+3的图象与x轴交于点A,与y轴交于点B,动点P从点B出发沿BA向终点A运动,同时动点Q从点O出发沿OB向点B运动,到达点B后立刻以原来的速度沿BO返回.点P,Q运动速度均为每秒1个单位长度,当点P到达点A时停止运动,点Q也同时停止.连结PQ,设运动时间为t(t>0)秒.
x+3的图象与x轴交于点A,与y轴交于点B,动点P从点B出发沿BA向终点A运动,同时动点Q从点O出发沿OB向点B运动,到达点B后立刻以原来的速度沿BO返回.点P,Q运动速度均为每秒1个单位长度,当点P到达点A时停止运动,点Q也同时停止.连结PQ,设运动时间为t(t>0)秒.
(1)求点P的坐标(用含t的代数式表示);
(2)当点Q从点O向点B运动时(未到达点B),是否存在实数t,使得△BPQ的面积大于17若存在,请求出t的取值范围;若不存在,请说明理由;
(3)伴随着P,Q两点的运动,线段PQ的垂直平分线为直线l.是否存在t的值,使得直线l经过点O?若存在,请求出所有t的值;若不存在,请说明理由.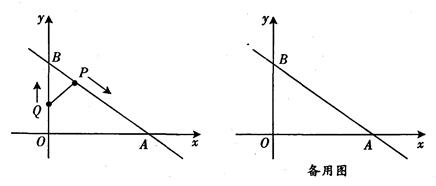
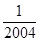

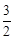
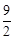
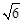
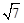
 中,自变量x的取值范围是
中,自变量x的取值范围是 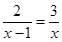 的解是
的解是 
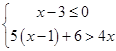
 ,其中x=2.
,其中x=2. x+m与抛物线y=
x+m与抛物线y=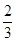 S△NBC,求直线MN的解析式;
S△NBC,求直线MN的解析式;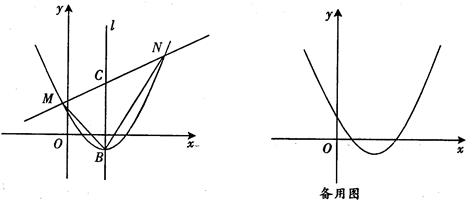
 粤公网安备 44130202000953号
粤公网安备 44130202000953号