某数学研究性学习小组制作了如下的三角函数计算图尺:在半径为1的半圆形量角器中,画一个直径为1的圆,把刻度尺 的0刻度固定在半圆的圆心 处,刻度尺可以绕点 旋转.从图中所示的图尺可读出 的值是

A. B. C. D.
如图, 是 的直径, 是 的切线,切点为 ,如果 ,则 的度数为
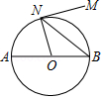
A. B. C. D.
如图, 是 的直径,弦 于 ,连接 ,过点 作 于 ,若 , ,则 的长度是
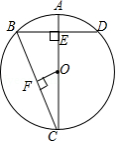
A. B. C. D.
如图, 是圆锥的母线, 为底面直径,已知 ,圆锥的侧面积为 ,则 的值为
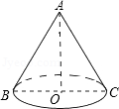
A. B. C. D.
如图,在 中, , , ,以点 为圆心, 长为半径画弧,交边 于点 ,则 的长为

A. B. C. D.
尺规作图特有的魅力曾使无数人沉湎其中.传说拿破仑通过下列尺规作图考他的大臣:
①将半径为 的 六等分,依次得到 , , , , , 六个分点;
②分别以点 , 为圆心, 长为半径画弧, 是两弧的一个交点;
③连接 .
问: 的长是多少?
大臣给出的正确答案应是

A. B. C. D.
如图, 的半径 ,以 为圆心, 为半径的弧交 于 、 点,则

A. B. C. D.
我们把1,1,2,3,5,8,13,21, 这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作 圆弧 , , , 得到斐波那契螺旋线,然后顺次连接 , , , 得到螺旋折线(如图),已知点 , , ,则该折线上的点 的坐标为
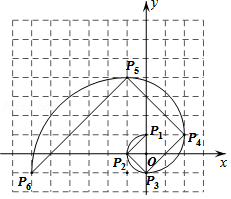
A. B. C. D.
运用图形变化的方法研究下列问题:如图, 是 的直径, 、 是 的弦,且 , , , .则图中阴影部分的面积是

A. B. C. D.
如图,在 中, , ,以 的中点 为圆心 分别与 , 相切于 , 两点,则 的长为

A. B. C. D.
如图,点 是以 为直径的半圆 的三等分点, ,则图中阴影部分的面积是
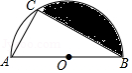
A. B. C. D.
如图,在半径为 的圆形铁片上切下一块高为 的弓形铁片,则弓形弦 的长为

A. B. C. D.