学习圆的性质后,小铭与小熹就讨论起来,小铭说:"被直径平分的弦也与直径垂直",小熹说:"用反例就能说明这是假命题".下列判断正确的是
| A. |
两人说的都对 |
| B. |
小铭说的对,小熹说的反例不存在 |
| C. |
两人说的都不对 |
| D. |
小铭说的不对,小熹说的反例存在 |
如图所示,点 , , 对应的刻度分别为1,3,5,将线段 绕点 按顺时针方向旋转,当点 首次落在矩形 的边 上时,记为点 ,则此时线段 扫过的图形的面积为

| A. |
|
B. |
6 |
C. |
|
D. |
|
往水平放置的半径为 的圆柱形容器内装入一些水以后,截面图如图所示,若水面宽度 ,则水的最大深度为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在 中, , ,点 在 上, ,以 为半径的 与 相切于点 ,交 于点 ,则 的长为
| A. |
|
B. |
|
C. |
|
D. |
1 |
如图,在边长为2的等边 中, 是 边上的中点,以点 为圆心, 为半径作圆与 , 分别交于 , 两点,则图中阴影部分的面积为

| A. |
|
B. |
|
C. |
|
D. |
|
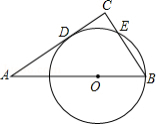
如图,点 , , , 均在 上,直径 ,点 是 的中点,点 关于 对称的点为 ,若 ,则弦 的长是

| A. |
|
B. |
2 |
C. |
|
D. |
1 |
如图, 是 的直径,点 为圆上一点, , 的平分线交 于点 , ,则 的直径为

| A. |
|
B. |
|
C. |
1 |
D. |
2 |
如图, 为 的直径,点 在 的延长线上, , 与 相切,切点分别为 , .若 , ,则 等于

| A. |
|
B. |
|
C. |
|
D. |
|
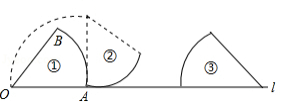
如图,放置在直线 上的扇形 .由图①滚动(无滑动)到图②,再由图②滚动到图③.若半径 , ,则点 所经过的运动路径的长是
A. B. C. D.
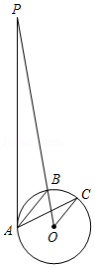
如图, 是 的切线,点 为切点, 交 于点 , ,点 在 上, .则 等于
| A. |
|
B. |
|
C. |
|
D. |
|