如图,在 中, , , , 分别为 、 、 的中点,则下列结论:① ,②四边形 为菱形,③ .其中正确的结论是 .(填写所有正确结论的序号)

请阅读下列材料,并完成相应的任务:
在数学中,利用图形在变化过程中的不变性质,常常可以找到解决问题的办法.著名美籍匈牙利数学家波利亚在他所著的《数学的发现》一书中有这样一个例子:请问如何在一个三角形 第一步,在 则有 下面是该结论的部分证明: 证明: 又
同理可得
|
任务:(1)请根据上面的操作步骤及部分证明过程,判断四边形的形状,并加以证明;
(2)请再仔细阅读上面的操作步骤,在(1)的基础上完成的证明过程;
(3)上述解决问题的过程中,通过作平行线把四边形放大得到四边形
,从而确定了点
,
的位置,这里运用了下面一种图形的变化是 .
.平移
.旋转
.轴对称
.位似
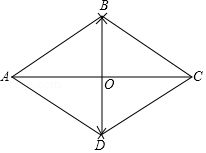
如图, 、 、 是 上的三点,且四边形 是菱形.若点 是圆上异于 、 、 的另一点,则 的度数是 .

如图,在等边三角形中,
,点
为边
的中点,点
为边
上的任意一点(不与点
,
重合),若点
关于直线
的对称点
恰好落在等边三角形
的边上,则
的长为
.
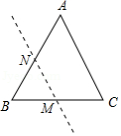
如图,在 中, ,点 、 分别是 、 的中点.
(1)求证: ;
(2)当四边形 为菱形时,求出该菱形的面积.

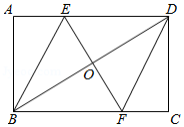
如图①,是矩形
的对角线,
,
.将
沿射线
方向平移到△
的位置,使
为
中点,连接
,
,
,
,如图②.
(1)求证:四边形是菱形;
(2)四边形的周长为 ;
(3)将四边形沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出所有可能拼成的矩形周长.

如图,已知线段 ,分别以 , 为圆心,大于 同样长为半径画弧,两弧交于点 , ,连接 , , , , ,则下列说法错误的是

A. 平分 B. 平分 C. D.
如图,在四边形中,
为一条对角线,
,
,
,
为
的中点,连接
.
(1)求证:四边形为菱形;
(2)连接,若
平分
,
,求
的长.

如图, ,分别以 、 为圆心,以长度5为半径作弧,两条弧分别相交于点 和 .依次连接 、 、 、 ,连接 交 于点 .
(1)判断四边形 的形状并说明理由;
(2)求 的长.
如图,四边形 是矩形, 、 分别是线段 、 上的点,点 是 与 的交点.若将 沿直线 折叠,则点 与点 重合.
(1)求证:四边形 是菱形;
(2)若 , ,求 的值.
如图,已知 .
(1)以点 为圆心,以适当长为半径画弧,交 于点 ,交 于点 .
(2)分别以 , 为圆心,以大于 的长为半径画弧,两弧在 的内部相交于点 .
(3)作射线 交 于点 .
(4)分别以 , 为圆心,以大于 的长为半径画弧,两弧相交于 , 两点.
(5)作直线 ,交 , 分别于点 , .
依据以上作图,若 , , ,则 的长是

| A. |
|
B. |
1 |
C. |
|
D. |
4 |
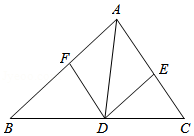
如图,在 中, 的角平分线交 于点 , , .
(1)试判断四边形 的形状,并说明理由;
(2)若 ,且 ,求四边形 的面积.
如图,四边形 是菱形,点 为对角线 的中点,点 在 的延长线上, ,垂足为 ,点 在 的延长线上, ,垂足为 ,
(1)若 ,求证:四边形 是菱形;
(2)若 , 的面积为16,求菱形 的面积.

如图,四边形 为矩形, 是对角线 的中点.连接 并延长至 ,使 ,以 , 为邻边作菱形 ,连接 .
(1)判断四边形 的形状,并证明你的结论.
(2)连接 ,若 ,求 的长.
