初中数学菱形的判定与性质试题

如图， $▱\mathit{ABCD}$ 的对角线 $\mathit{AC}$ ， $\mathit{BD}$ 交于点 $E$ ，以 $\mathit{AB}$ 为直径的 $\odot O$ 经过点 $E$ ，与 $\mathit{AD}$ 交于点 $F$ ， $G$ 是 $\mathit{AD}$ 延长线上一点，连接 $\mathit{BG}$ ，交 $\mathit{AC}$ 于点 $H$ ，且 $\angle \mathit{DBG}=\frac{1}{2}\angle \mathit{BAD}$ ．

（1）求证： $\mathit{BG}$ 是 $\odot O$ 的切线；

（2）若 $\mathit{CH}=3$ ， $\tan \angle \mathit{DBG}=\frac{1}{2}$ ，求 $\odot O$ 的直径．

能够完全重合的平行四边形纸片 $\mathit{ABCD}$ 和 $\mathit{AEFG}$ 按图①方式摆放，其中 $\mathit{AD}=\mathit{AG}=5$ ， $\mathit{AB}=9$ ．点 $D$ ， $G$ 分别在边 $\mathit{AE}$ ， $\mathit{AB}$ 上， $\mathit{CD}$ 与 $\mathit{FG}$ 相交于点 $H$ ．

【探究】求证：四边形 $\mathit{AGHD}$ 是菱形．

【操作一】固定图①中的平行四边形纸片 $\mathit{ABCD}$ ，将平行四边形纸片 $\mathit{AEFG}$ 绕着点 $A$ 顺时针旋转一定的角度，使点 $F$ 与点 $C$ 重合，如图②．则这两张平行四边形纸片未重叠部分图形的周长和为 　    　．

【操作二】将图②中的平行四边形纸片 $\mathit{AEFG}$ 绕着点 $A$ 继续顺时针旋转一定的角度，使点 $E$ 与点 $B$ 重合，连接 $\mathit{DG}$ ， $\mathit{CF}$ ，如图③，若 $\sin \angle \mathit{BAD}=\frac{4}{5}$ ，则四边形 $\mathit{DCFG}$ 的面积为 　　．

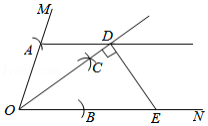
如图，已知是一个锐角，以点为圆心，任意长为半径画弧，分别交、于点、，再分别以点、为圆心，大于长为半径画弧，两弧交于点，画射线．过点作，交射线于点，过点作，交于点．设，，则　　．

如图，在四边形中，，对角线的垂直平分线与边、分别相交于点、．

（1）求证：四边形是菱形；

（2）若，，求菱形的周长．

如图，在菱形 $\mathit{ABCD}$ 中，将对角线 $\mathit{AC}$ 分别向两端延长到点 $E$ 和 $F$ ，使得 $\mathit{AE}=\mathit{CF}$ ．连接 $\mathit{DE}$ ， $\mathit{DF}$ ， $\mathit{BE}$ ， $\mathit{BF}$ ．

求证：四边形 $\mathit{BEDF}$ 是菱形．

菱形 $\mathit{ABCD}$ 的对角线 $\mathit{AC}$ ， $\mathit{BD}$ 相交于点 $O$ ， $0°<\angle \mathit{ABO}⩽60°$ ，点 $G$ 是射线 $\mathit{OD}$ 上一个动点，过点 $G$ 作 $\mathit{GE}//\mathit{DC}$ 交射线 $\mathit{OC}$ 于点 $E$ ，以 $\mathit{OE}$ ， $\mathit{OG}$ 为邻边作矩形 $\mathit{EOGF}$ ．

（1）如图1，当点 $F$ 在线段 $\mathit{DC}$ 上时，求证： $\mathit{DF}=\mathit{FC}$ ；

（2）若延长 $\mathit{AD}$ 与边 $\mathit{GF}$ 交于点 $H$ ，将 $\mathit{\Delta GDH}$ 沿直线 $\mathit{AD}$ 翻折 $180°$ 得到 $\mathit{\Delta MDH}$ ．

①如图2，当点 $M$ 在 $\mathit{EG}$ 上时，求证：四边形 $\mathit{EOGF}$ 为正方形；

②如图3，当 $\tan \angle \mathit{ABO}$ 为定值 $m$ 时，设 $\mathit{DG}=k·\mathit{DO}$ ， $k$ 为大于0的常数，当且仅当 $k>2$ 时，点 $M$ 在矩形 $\mathit{EOGF}$ 的外部，求 $m$ 的值．

如图，矩形纸片 $\mathit{ABCD}$ 中， $\mathit{AB}=6$ ， $\mathit{BC}=12$ ．将纸片折叠，使点 $B$ 落在边 $\mathit{AD}$ 的延长线上的点 $G$ 处，折痕为 $\mathit{EF}$ ，点 $E$ 、 $F$ 分别在边 $\mathit{AD}$ 和边 $\mathit{BC}$ 上．连接 $\mathit{BG}$ ，交 $\mathit{CD}$ 于点 $K$ ， $\mathit{FG}$ 交 $\mathit{CD}$ 于点 $H$ ．给出以下结论：

① $\mathit{EF}\perp \mathit{BG}$ ；

② $\mathit{GE}=\mathit{GF}$ ；

③ $\mathit{\Delta GDK}$ 和 $\mathit{\Delta GKH}$ 的面积相等；

④当点 $F$ 与点 $C$ 重合时， $\angle \mathit{DEF}=75°$ ，

其中正确的结论共有 $($ 　　 $)$

A．

1个

B．

2个

C．

3个

D．

4个

如图， $\mathit{\Delta ABD}$ 中， $\angle \mathit{ABD}=\angle \mathit{ADB}$ ．

（1）作点 $A$ 关于 $\mathit{BD}$ 的对称点 $C$ ；（要求：尺规作图，不写作法，保留作图痕迹）

（2）在（1）所作的图中，连接 $\mathit{BC}$ ， $\mathit{DC}$ ，连接 $\mathit{AC}$ ，交 $\mathit{BD}$ 于点 $O$ ．

①求证：四边形 $\mathit{ABCD}$ 是菱形；

②取 $\mathit{BC}$ 的中点 $E$ ，连接 $\mathit{OE}$ ，若 $\mathit{OE}=\frac{13}{2}$ ， $\mathit{BD}=10$ ，求点 $E$ 到 $\mathit{AD}$ 的距离．

如图，先有一张矩形纸片，，，点，分别在矩形的边，上，将矩形纸片沿直线折叠，使点落在矩形的边上，记为点，点落在处，连接，交于点，连接．下列结论：

①；

②四边形是菱形；

③，重合时，；

④的面积的取值范围是．

其中正确的是　　（把正确结论的序号都填上）．

如图，矩形中，，，点是对角线的中点，过点的直线分别交、边于点、．

（1）求证：四边形是平行四边形；

（2）当时，求的长．

如图，四边形 ABCD的对角线相交于点 O，且点 O是 BD的中点，若 AB＝ AD＝5， BD＝8，∠ ABD＝∠ CDB，则四边形 ABCD的面积为（　　）

A．

40

B．

24

C．

20

D．

15

如图，在中，是斜边的中点，以为直径作圆交于点，延长至，使，连接、，交圆于点．

（1）判断四边形的形状，并说明理由；

（2）求证：；

（3）若，，求的长．

如图，将沿着边翻折，得到，且．

（1）判断四边形的形状，并说明理由；

（2）若，，求四边形的面积．

规定：如果一个四边形有一组对边平行，一组邻边相等，那么称此四边形为广义菱形．根据规定判断下面四个结论：①正方形和菱形都是广义菱形；②平行四边形是广义菱形；③对角线互相垂直，且两组邻边分别相等的四边形是广义菱形；④若、的坐标分别为，，是二次函数的图象上在第一象限内的任意一点，垂直直线于点，则四边形是广义菱形．其中正确的是　　．（填序号）

如图，面积为24的 $▱\mathit{ABCD}$ 中，对角线 $\mathit{BD}$ 平分 $\angle \mathit{ABC}$ ，过点 $D$ 作 $\mathit{DE}\perp \mathit{BD}$ 交 $\mathit{BC}$ 的延长线于点 $E$ ， $\mathit{DE}=6$ ，则 $\sin \angle \mathit{DCE}$ 的值为 $($ 　　 $)$

A．

$\frac{24}{25}$

B．

$\frac{4}{5}$

C．

$\frac{3}{4}$

D．

$\frac{12}{25}$