如图, 中, , 垂直平分 ,交线段 于点 (点 与点 不重合),点 为 上一点,点 为 上一点(点 与点 不重合),且 .
(1)如图1,当 时,线段 和 的数量关系是 .
(2)如图2,当 时,猜想线段 和 的数量关系,并加以证明.
(3)若 , , ,请直接写出 的长.

已知,在 中, , 是 边上一点,连接 ,分别以 和 为直角边作 和 ,使 ,点 , 在 下方,连接 .
(1)如图1,当 , , 时,
求证:① ,② ;
(2)如图2,当 , , 时,猜想 和 之间的数量关系?并说明理由.
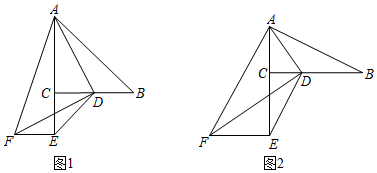
如图, 是等腰直角三角形, , 是射线 上一点(点 不与点 重合),以 为斜边作等腰直角三角形 (点 和点 在 的同侧),连接 .
(1)如图①,当点 与点 重合时,直接写出 与 的位置关系;
(2)如图②,当点 与点 不重合时,(1)的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;
(3)当 时,请直接写出 的值.

如图,是具有公共边 的两个直角三角形,其中, , .
(1)如图1,若延长 到点 ,使 ,连接 , .
①求证: , ;
②求证: ;
(2)若 与 位置如图2所示,请直接写出线段 , , 的数量关系.

已知:在 外分别以 , 为边作 与 .
(1)如图1, 与 分别是以 , 为斜边的等腰直角三角形,连接 .以 为直角边构造 ,且 ,连接 , , .
求证:① .
②四边形 是平行四边形.
(2)小明受到图1的启发做了进一步探究:
如图2,在 外分别以 , 为斜边作 与 ,并使 ,取 的中点 ,连接 , 后发现,两者间存在一定的数量关系且夹角度数一定,请你帮助小明求出 的值及 的度数.
(3)小颖受到启发也做了探究:
如图3,在 外分别以 , 为底边作等腰三角形 和等腰三角形 ,并使 ,取 的中点 ,连接 , 后发现,当给定 时,两者间也存在一定的数量关系且夹角度数一定,若 , ,请你帮助小颖用含 , 的代数式直接写出 的值,并用含 的代数式直接表示 的度数.

已知:在 中, ,点 是 边上一点,连接 ,点 是线段 延长线上一点,连接 , ,使 ,过点 作 ,交 于点 .
(1)①如图1,当 时,线段 与 之间的数量关系是 .
②如图2,当 时,线段 与 之间的数量关系是 .
(2)如图3,当 时,线段 与 之间具有怎样的数量关系?请说明理由.
(3)如图4,当 时,直接写出线段 与 之间的数量关系.(用含 的式子表示)

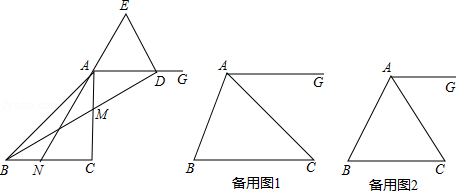
已知: 是等腰三角形, , .点 在边 上,点 在边 上(点 、点 不与所在线段端点重合), ,连接 , ,射线 ,延长 交射线 于点 ,点 在直线 上,且 .
(1)如图,当 时
①求证: ;
②求 的度数;
(2)当 ,其它条件不变时, 的度数是 ;(用含 的代数式表示)
(3)若 是等边三角形, ,点 是 边上的三等分点,直线 与直线 交于点 ,请直接写出线段 的长.
在 中, ,点 是 的中点,点 是 上的一个动点(点 不与点 , , 重合).过点 ,点 作直线 的垂线,垂足分别为点 和点 ,连接 , .
(1)如图1,请直接写出线段 与 的数量关系;
(2)如图2,当 时,请判断线段 与 之间的数量关系和位置关系,并说明理由
(3)若 , ,当 为等腰三角形时,请直接写出线段 的长.

如图,在 中, , , 于点 .
(1)如图1,点 , 在 , 上,且 .求证: ;
(2)点 , 分别在直线 , 上,且 .
①如图2,当点 在 的延长线上时,求证: ;
②当点 在点 , 之间,且 时,已知 ,直接写出线段 的长.

如图 为等边三角形,以 为边在 外作正方形 ,延长 分别交 、 的延长线于点 , , 于点 , 于点 ,连接 .
(1)判断 和 是否全等,并说明理由;
(2)求证: ;
(3)已知 ,若点 是直线 上的动点,请直接写出 周长的最小值.

阅读下面材料:
小明遇到这样一个问题:
如图1, 中, ,点 在 上,且 ,求证: .
小明发现,除了直接用角度计算的方法外,还可以用下面两种方法:
方法1:如图2,作 平分 ,与 相交于点 .
方法2:如图3,作 ,与 相交于点 .
(1)根据阅读材料,任选一种方法,证明 .
用学过的知识或参考小明的方法,解决下面的问题:
(2)如图4, 中,点 在 上,点 在 上,且 ,点 在 上,且 ,延长 、 ,相交于点 ,且 .
①在图中找出与 相等的角,并加以证明;
②若 ,猜想线段 与 的数量关系,并证明你的猜想.

在 中, , , ,若 ,如图1,则有 ;若 为锐角三角形时,小明猜想: ,理由如下:如图2,过点 作 于点 ,设 .在 中, ,在 中,
,
当 为锐角三角形时,
所以小明的猜想是正确的.
(1)请你猜想,当 为钝角三角形时, 与 的大小关系.
(2)温馨提示:在图3中,作 边上的高.
(3)证明你猜想的结论是否正确.

(1)阅读理解:
如图①,在 中,若 , ,求 边上的中线 的取值范围.
解决此问题可以用如下方法:延长 到点 使 ,再连接 (或将 绕着点 逆时针旋转 得到 ,把 、 , 集中在 中,利用三角形三边的关系即可判断.
中线 的取值范围是 ;
(2)问题解决:
如图②,在 中, 是 边上的中点, 于点 , 交 于点 , 交 于点 ,连接 ,求证: ;
(3)问题拓展:
如图③,在四边形 中, , , ,以 为顶点作一个 角,角的两边分别交 , 于 、 两点,连接 ,探索线段 , , 之间的数量关系,并加以证明.

阅读下列材料并回答问题:
材料1:如果一个三角形的三边长分别为 , , ,记 ,那么三角形的面积为 . ①
古希腊几何学家海伦 ,约公元50年),在数学史上以解决几何测量问题而闻名.他在《度量》一书中,给出了公式①和它的证明,这一公式称海伦公式.
我国南宋数学家秦九韶(约 约 ,曾提出利用三角形的三边求面积的秦九韶公式: . ②
下面我们对公式②进行变形: .
这说明海伦公式与秦九韶公式实质上是同一公式,所以我们也称①为海伦 秦九韶公式.
问题:如图,在 中, , , , 内切于 ,切点分别是 、 、 .
(1)求 的面积;
(2)求 的半径.
