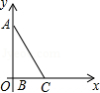
《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示, 中, , , ,求 的长,如果设 ,则可列方程为 .
对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形 ,对角线 、 交于点 .若 , ,则 .

如图,点 , 在半圆的直径 上,点 , 在 上,四边形 为正方形.若半圆的半径为 ,则正方形的边长为 .

《九章算术》中一道"引葭赴岸"问题:"今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?"题意是:有一个池塘,其地面是边长为10尺的正方形,一棵芦苇 生长在它的中央,高出水面部分 为1尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部 恰好碰到岸边的 处(如图),水深和芦苇长各多少尺?则该问题的水深是 尺.

如图,在正方形 内作 , 交 于点 , 交 于点 ,连接 ,过点 作 ,垂足为 ,将 绕点 顺时针旋转 得到 ,若 , ,则 的长为 .

如图,在 的正方形方格图形中,小正方形的顶点称为格点, 的顶点都在格点上,则 的正弦值是 .

如图,在四边形ABCD中,对角线AC、BD相交于点E, , , , ,则AE= (提示:可过点A作BD的垂线)

如图是一块圆环形玉片的残片,作外圆的弦 与内圆相切于点 ,量得 、点 与 的中点 的距离 .则此圆环形玉片的外圆半径为 .

如图的三角形纸片中,AB=AC,BC=12cm,∠C=30°,折叠这个三角形,使点B落在AC的中点D处,折痕为EF,那么BF的长为 cm.

如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据: 米, 米, , ,则警示牌的高 为 米(结果精确到0.1米,参考数据: , .

勘测队按实际需要构建了平面直角坐标系,并标示了,
,
三地的坐标,数据如图(单位:
.笔直铁路经过
,
两地.
(1),
间的距离为
;
(2)计划修一条从到铁路
的最短公路
,并在
上建一个维修站
,使
到
,
的距离相等,则
,
间的距离为
.

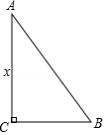
在 中, , , .如图,将直角顶点 放在原点,点 放在 轴正半轴上,当点 在 轴上向右移动时,点 也随之在 轴上向下移动,当点 到达原点时,点 停止移动,在移动过程中,点 到原点的最大距离为 .