把两个同样大小的含 角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个的直角顶点重合于点 ,且另三个锐角顶点 , , 在同一直线上.若 ,则 .

把两个同样大小的含 角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个的直角顶点重合于点 ,且另三个锐角顶点 , , 在同一直线上.若 ,则 .
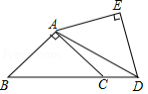
如图,已知 ,以 为直角边作等腰直角三角形 ,再以 为直角边作等腰直角三角形 ,如此下去,则线段 的长度为 .

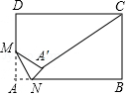
如图,在矩形 中, , , 是 边的中点, 是 边上的动点,将 沿 所在直线折叠,得到△ ,连接 ,则 的最小值是 .
《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示, 中, , , ,求 的长,如果设 ,则可列方程为 .
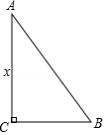
如图,在 中, , 边上的高为4,在 的内部作一个矩形 ,使 在 边上,另外两个顶点分别在 、 边上,则对角线 长的最小值为 .

如图,点 , 在半圆的直径 上,点 , 在 上,四边形 为正方形.若半圆的半径为 ,则正方形的边长为 .

如图,在正方形 内作 , 交 于点 , 交 于点 ,连接 ,过点 作 ,垂足为 ,将 绕点 顺时针旋转 得到 ,若 , ,则 的长为 .

如图,在四边形ABCD中,对角线AC、BD相交于点E, , , , ,则AE= (提示:可过点A作BD的垂线)

如图的三角形纸片中,AB=AC,BC=12cm,∠C=30°,折叠这个三角形,使点B落在AC的中点D处,折痕为EF,那么BF的长为 cm.

《九章算术》是中国传统数学的重要著作之一,奠定了中国传统数学的基本框架.如图所示是其中记载的一道"折竹"问题:"今有竹高一丈,末折抵地,去根三尺,问折者高几何?"题意是:一根竹子原高1丈 丈 尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?答:折断处离地面 尺高.
