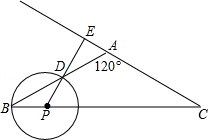
如图, 中, , . 是底边 上的一个动点 与 、 不重合),以 为圆心, 为半径的 与射线 交于点 ,射线 交射线 于点 .
(1)若点 在线段 的延长线上,设 , ,求 关于 的函数关系式,并写出 的取值范围.
(2)当 时,试说明射线 与 是否相切.
(3)连接 ,若 ,求 的长.
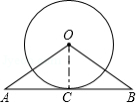
如图,在 中, , ,斜边 的两个端点分别在相互垂直的射线 、 上滑动,下列结论:
①若 、 两点关于 对称,则 ;
② 、 两点距离的最大值为4;
③若 平分 ,则 ;
④斜边 的中点 运动路径的长为 ;
其中正确的是 (把你认为正确结论的序号都填上).

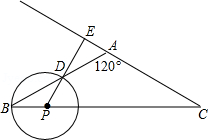
如图, 中, , . 是底边 上的一个动点 与 、 不重合),以 为圆心, 为半径的 与射线 交于点 ,射线 交射线 于点 .
(1)若点 在线段 的延长线上,设 , ,求 关于 的函数关系式,并写出 的取值范围.
(2)当 时,试说明射线 与 是否相切.
(3)连接 ,若 ,求 的长.
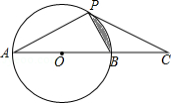
已知:如图,在 中, , 与 相切于点 .求证: .小明同学的证明过程如下框:
证明:连结 , , , 又 , , . |
小明的证法是否正确?若正确,请在框内打“ ”;若错误,请写出你的证明过程.
如图,已知 是 的直径,点 为圆上一点,点 为 延长线上一点, , .
(1)求证: 是 的切线.
(2)若 的直径为8,求阴影部分的面积.
如图,在 中, ,点 、 分别是线段 、 的中点,过点 作 的平行线交 的延长线于点 ,连接 .
(1)求证: ;
(2)求证:四边形 为矩形.

如图,等腰 中, ,边 的垂直平分线交 于点 ,交 于点 .若 的周长为26,则 的长为 .

如图, 是半圆 的直径, 是半圆上的一点, 平分 交半圆于点 ,过点 作 与 的延长线交于点 .
(1)求证: 是半圆的切线;
(2)若 , ,求半圆的直径.

如图,在 中, ,过 延长线上的点 作 ,交 的延长线于点 ,以 为圆心, 长为半径的圆过点 .
(1)求证:直线 与 相切;
(2)若 , 的半径为12,则 .

如图,在 中, , ,分别以点 , 为圆心, 的长为半径作弧,两弧交于点 ,连接 , ,则四边形 的面积为

A. B.9C.6D.
函数 的图象与 轴、 轴分别交于 、 两点,点 在 轴上.若 为等腰三角形,则满足条件的点 共有 个.