如图,在矩形 中, ,点 是 的中点,点 在 上, ,点 、 在线段 上.若 是等腰三角形且底角与 相等,则 .

如图,四边形 为矩形, 是对角线 的中点.连接 并延长至 ,使 ,以 , 为邻边作菱形 ,连接 .
(1)判断四边形 的形状,并证明你的结论.
(2)连接 ,若 ,求 的长.

如图,在 中, 为直径, .点 为弦 的中点,点 为 上任意一点.则 的大小可能是
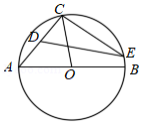
A. B. C. D.
如图,已知 、 为 的两条直径, 为切线,过 上一点 作 于 ,连接 并延长交 于点 ,连接 .
(1)求证: .
(2)设 为点 关于 对称点,连接 、 ,如果 , 的半径为3,求 的值.

如图,把 沿 翻折得 .
(1)连接 ,则 与 的位置关系是 .
(2)不在原图中添加字母和线段,只加一个条件使四边形 是平行四边形,写出添加的条件,并说明理由.

如图, 是 的直径, 为弦, 的平分线交 于点 ,过点 的切线交 的延长线于点 .
求证:(1) ;
(2) .

如图,在 中, , 和 关于直线 对称,连接 ,与 相交于点 ,过点 作 ,垂足为 , 相交于点 ,若 , ,则 的值为

| A. |
|
B. |
|
C. |
|
D. |
|
数学课上,张老师举了下面的例题:
例1 等腰三角形 中, ,求 的度数.(答案:
例2 等腰三角形 中, ,求 的度数,(答案: 或 或
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形 中, ,求 的度数.
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现, 的度数不同,得到 的度数的个数也可能不同,如果在等腰三角形 中,设 ,当 有三个不同的度数时,请你探索 的取值范围.
如图,四边形 为平行四边形,连接 ,且 .请用尺规完成基本作图:作出 的角平分线与 交于点 .连接 交 于点 ,交 于点 ,猜想线段 和线段 的数量关系,并证明你的猜想.(尺规作图保留作图痕迹,不写作法)

如图,在 中, , .分别以点 , 为圆心,大于 的长为半径画弧,两弧交于 , 两点,直线 交 于点 ,连接 .以点 为圆心, 为半径画弧,交 延长线于点 ,连接 .若 ,则 的周长为 .

如图,在 中, , 和 关于直线 对称,连接 ,与 相交于点 ,过点 作 ,垂足为 , 相交于点 ,若 , ,则 的值为

A. B. C. D.
如图,在 中, , ,点 是 边上任意一点,过点 作 交 于点 ,则 的度数是
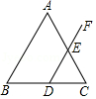
A. B. C. D.