如图,在 中,过 点作 于点 ,交 于点 ,过 点作 于点 ,交 于点 .
(1)求证:四边形 是平行四边形;
(2)已知 , ,求 的长.
在等边 中,

(1)如图1, , 是 边上的两点, , ,求 的度数;
(2)点 , 是 边上的两个动点(不与点 , 重合),点 在点 的左侧,且 ,点 关于直线 的对称点为 ,连接 , .
①依题意将图2补全;
②小茹通过观察、实验提出猜想:在点 , 运动的过程中,始终有 ,小茹把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证明 ,只需证 是等边三角形;
想法2:在 上取一点 ,使得 ,要证明 ,只需证 ;
想法3:将线段 绕点 顺时针旋转 ,得到线段 ,要证 ,只需证 ,
请你参考上面的想法,帮助小茹证明 (一种方法即可).
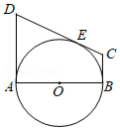
如图所示,直线 和圆 相切于点 ,交直径 的延长线于点 .过点 作 的垂线,交 于点 ,交圆 于点 .作平行四边形 ,连接 , , .
(1)求证: ;
(2)求 及 的大小.

如图,在正方形 ABCD中, AB=6, M是对角线 BD上的一个动点(0< DM< BD),连接 AM,过点 M作 MN⊥ AM交 BC于点 N.
(1)如图①,求证: MA= MN;
(2)如图②,连接 AN, O为 AN的中点, MO的延长线交边 AB于点 P,当 时,求 AN和 PM的长;
(3)如图③,过点 N作 NH⊥ BD于 H,当 AM=2 时,求△ HMN的面积.

如图,在 中,各内角的平分线分别相交于点 , , , .
(1)求证: ;
(2)猜一猜:四边形 是什么样的特殊四边形?证明你的猜想;
(3)若 , , ,求四边形 的面积.

数学课上,探讨角平分线的作法时,李老师用直尺和圆规作角平分线,方法如下:

小颖的身边只有刻度尺,经过尝试,她发现利用刻度尺也可以作角平分线.
根据以上情境,解决下列问题:
①李老师用尺规作角平分线时,用到的三角形全等的判定方法是_________.
②小聪的作法正确吗?请说明理由.
③请你帮小颖设计用刻度尺作角平分线的方法.(要求:作出图形,写出作图步骤,不予证明)
如图,P为等腰△ABC的顶角A的外角平分线上任一点,连接PB,PC.
(1)求证:PB+PC>2AB.
(2)当PC=2,PB= ,∠ACP=45°时,求AB的长.
,∠ACP=45°时,求AB的长.
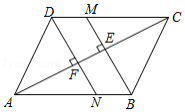
如图,在 中, , 是对角线 上的两点(点 在点 左侧),且 .
(1)求证:四边形 是平行四边形;
(2)当 , , 时,求 的长.

如图, 是正方形 的对角线,线段 在其所在的直线上平移,将平移得到的线段记为 ,连接 ,过点 作 ,垂足为 ,连接 、 .
(1)如图①所示,求证: ;
(2)如图②所示, 在 的延长线上,如图③所示, 在 的反向延长线上,猜想线段 、 之间有怎样的数量关系?请直接写出你的猜想,不需证明.

如图,在⊙ O中, B是⊙ O上的一点,∠ ABC=120°,弦 AC=2 ,弦 BM平分∠ ABC交 AC于点 D,连接 MA, MC.
(1)求⊙ O半径的长;
(2)求证: AB+ BC= BM.

如图,在矩形 中,点 在边 上,点 在 的延长线上,且 .
求证:(1) ;
(2)四边形 是平行四边形.

如图,△ ABC中, D是 BC边上一点, E是 AD的中点,过点 A作 BC的平行线交 BE的延长线于 F,且 AF= CD,连接 CF.
(1)求证:△ AEF≌△ DEB;
(2)若 AB= AC,试判断四边形 ADCF的形状,并证明你的结论.

如图所示, 是 的直径, 和 分别切 于 , 两点, 与 有公共点 ,且 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.