如图,在 和 中, , ,点 , , 依次在同一直线上,且 .
(1)求证: .
(2)连结 ,当 , 时,求 的长.

已知: 在 中, , 为 的中点, , ,垂足分别为点 , ,且 . 求证: 是等边三角形 .

如图,四边形 内接于 , ,延长 到点 ,使得 ,连接 .
(1)求证: ;
(2)若 , , ,求 的值.

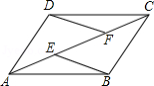
已知:如图, 、 是平行四边形 的对角线 上的两点, .
求证:(1) ;
(2) .
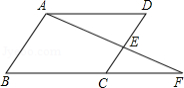
如图,点 是 的边 的中点,连结 并延长,交 的延长线于点 .
(1)若 的长为2,求 的长.
(2)若 ,试添加一个条件,并写出 的度数.
问题背景
如图1,在正方形 的内部,作 ,根据三角形全等的条件,易得 ,从而得到四边形 是正方形.
类比探究
如图2,在正 的内部,作 , , , 两两相交于 , , 三点 , , 三点不重合)
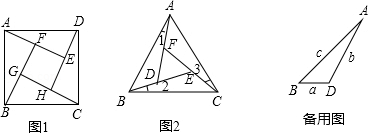
(1) , , 是否全等?如果是,请选择其中一对进行证明.
(2) 是否为正三角形?请说明理由.
(3)进一步探究发现, 的三边存在一定的等量关系,设 , , ,请探索 , , 满足的等量关系.
如图,在平行四边形 中, 为 边的中点,连接 ,若 的延长线和 的延长线相交于点 .
(1)求证: ;
(2)连接 和 相交于点为 ,若 的面积为2,求平行四边形 的面积.

已知正方形 的对角线 , 相交于点 .
(1)如图1, , 分别是 , 上的点, 与 的延长线相交于点 .若 ,求证: ;
(2)如图2, 是 上的点,过点 作 ,交线段 于点 ,连接 交 于点 ,交 于点 .若 ,
①求证: ;
②当 时,求 的长.

在一次数学研究性学习中,小兵将两个全等的直角三角形纸片 和 拼在一起,使点 与点 重合,点 与点 重合(如图 ,其中 , , ,并进行如下研究活动.
活动一:将图1中的纸片 沿 方向平移,连结 , (如图 ,当点 与点 重合时停止平移.
[思考]图2中的四边形 是平行四边形吗?请说明理由.
[发现]当纸片 平移到某一位置时,小兵发现四边形 为矩形(如图 .求 的长.
活动二:在图3中,取 的中点 ,再将纸片 绕点 顺时针方向旋转 度 ,连结 , (如图 .
[探究]当 平分 时,探究 与 的数量关系,并说明理由.

如图,在 中, , 是对角线 上的两点(点 在点 左侧),且 .
(1)求证:四边形 是平行四边形;
(2)当 , , 时,求 的长.

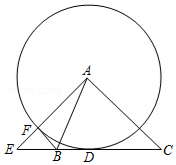
如图,在 中, , 与 相切于点 ,过点 作 的垂线交 的延长线于点 ,交 于点 ,连结 .
(1)求证: 是 的切线.
(2)若 , ,求 的长.
如图, 为等腰直角三角形,延长 至点 使 , 是矩形,其对角线 , 交于点 ,连接 交 于点 .
(1)求证: ;
(2)求 的值.

已知:如图,四边形 为平行四边形,点 、 、 、 在同一直线上, .
求证:(1) ;
(2) .
