如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为 ,另两张直角三角形纸片的面积都为 ,中间一张正方形纸片的面积为 ,则这个平行四边形的面积一定可以表示为

A. B. C. D.
如图,矩形 中, , ,点 在对角线 上,且 ,连接 并延长,交 的延长线于点 ,连接 ,则 的长为 .

如图,在 中, , , ,点 在线段 上,且 , 是线段 上的一点,连接 ,把四边形 沿直线 翻折,得到四边形 ,当点 恰好落在线段 上时, .

如图,点 , , , 共线, , ,添加一个条件,不能判断 的是

| A. |
|
B. |
|
C. |
|
D. |
|
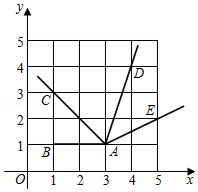
如图,在直角坐标系中,以点 为端点的四条射线 , , , 分别过点 ,点 ,点 ,点 ,则 (填" "、" "、" "中的一个).
等腰三角形的一边长是3,另两边的长是关于 的方程 的两个根,则 的值为
A.3B.4C.3或4D.7
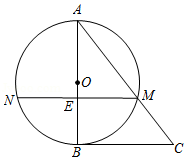
如图,在 中,以 为直径的 交 于点 ,弦 交 于点 ,且 , , .
(1)求证: 是 的切线;
(2)求 的直径 的长度.
如图,在 中, , , 的半径为1,点 是 边上的动点,过点 作 的一条切线 (其中点 为切点),则线段 长度的最小值为 .

如图,在正方形 中,点 是 上一动点(不与 、 重合),对角线 、 相交于点 ,过点 分别作 、 的垂线,分别交 、 于点 、 ,交 、 于点 、 .下列结论:
① ;
② ;
③ ;
④ ;
⑤点 在 、 两点的连线上.
其中正确的是

A.①②③④B.①②③⑤C.①②③④⑤D.③④⑤
如图1,点 从 的顶点 出发,沿 匀速运动到点 ,图2是点 运动时线段 的长度 随时间 变化的关系图象,其中点 为曲线部分的最低点,则 的边 的长度为

A.12B.8C.10D.13