如图,在矩形 中,对角线 与 相交于点 , ,对角线 所在的直线绕点 顺时针旋转角 ,所得的直线 分别交 , 于点 , .
(1)求证: ;
(2)当旋转角 为多少度时,四边形 为菱形?试说明理由.

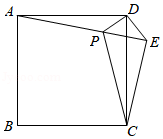
如图,在正方形 外取一点 ,连接 , , ,过点 作 的垂线交 于点 ,若 , .下列结论:① ;② ;③点 到直线 的距离为 ;④ ,其中正确结论的序号为 .
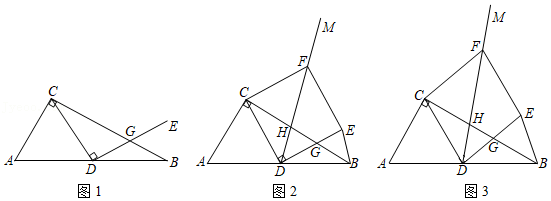
如图,在 中, , ,点 为 的中点,连接 ,将线段 绕点 顺时针旋转 得到线段 ,且 交线段 于点 , 的平分线 交 于点 .
(1)如图1,若 ,则线段 与 的数量关系是 , ;
(2)如图2,在(1)的条件下,过点 作 交 于点 ,连接 , .
①试判断四边形 的形状,并说明理由;
②求证: ;
(3)如图3,若 , ,过点 作 交 于点 ,连接 , ,请直接写出 的值(用含 的式子表示).
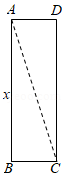
《九章算术》是我国古代数学名著,书中有下列问题:"今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?"其意思为:今有一门,高比宽多6尺8寸,门对角线距离恰好为1丈.问门高、宽各是多少? 丈 尺,1尺 寸)如图,设门高 为 尺,根据题意,可列方程为 .
如图,已知点 , , , 在同一条直线上, , , .
(1)求证: .
(2)判断四边形 的形状,并证明.

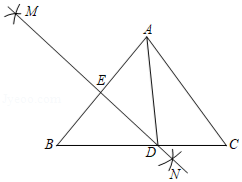
如图,在 中, ,分别以点 , 为圆心,大于 的长为半径画弧,两弧相交于点 和点 ,作直线 分别交 、 于点 和点 ,若 ,则 的度数是
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在正方形 中,对角线 , 相交于点 ,点 , 是对角线 上的两点,且 .连接 , , , .
(1)证明: .
(2)若 , ,求四边形 的周长.

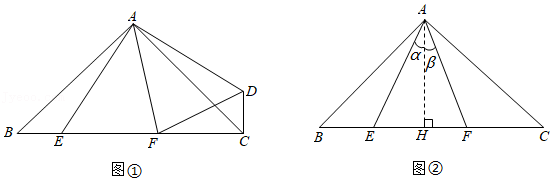
如图①, 、 是等腰 的斜边 上的两动点, , 且 .
(1)求证: ;
(2)求证: ;
(3)如图②,作 ,垂足为 ,设 , ,不妨设 ,请利用(2)的结论证明:当 时, 成立.
已知:如图,四边形 为平行四边形,点 、 、 、 在同一直线上, .
求证:(1) ;
(2) .
