如图,将 绕点 逆时针旋转到 的位置,使点 落在 上, 与 交于点 .若 , , ,则 的长为 .

如图,在平面直角坐标系中, 的边 , 的中点 , 的横坐标分别是1,4,则点 的横坐标是 .

在数学兴趣小组活动中,小亮进行数学探究活动.
(1) 是边长为3的等边三角形, 是边 上的一点,且 ,小亮以 为边作等边三角形 ,如图1.求 的长;

(2) 是边长为3的等边三角形, 是边 上的一个动点,小亮以 为边作等边三角形 ,如图2.在点 从点 到点 的运动过程中,求点 所经过的路径长;
(3) 是边长为3的等边三角形, 是高 上的一个动点,小亮以 为边作等边三角形 ,如图3.在点 从点 到点 的运动过程中,求点 所经过的路径长;

(4)正方形 的边长为3, 是边 上的一个动点,在点 从点 到点 的运动过程中,小亮以 为顶点作正方形 ,其中点 、 都在直线 上,如图4.当点 到达点 时,点 、 、 与点 重合.则点 所经过的路径长为 ,点 所经过的路径长为 .
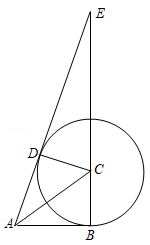
如图, 中, ,以点 为圆心, 为半径作 , 为 上一点,连接 、 , , 平分 .
(1)求证: 是 的切线;
(2)延长 、 相交于点 ,若 ,求 的值.
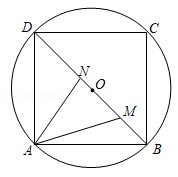
如图,正方形 内接于 ,线段 在对角线 上运动,若 的面积为 , ,则 周长的最小值是
| A. |
3 |
B. |
4 |
C. |
5 |
D. |
6 |
在平面直角坐标系 中,对于 、 两点,若在 轴上存在点 ,使得 ,且 ,则称 、 两点互相关联,把其中一个点叫做另一个点的关联点.已知点 、 ,点 在一次函数 的图象上.
(1)①如图,在点 、 、 中,点 的关联点是 (填" "、" "或" " ;
②若在线段 上存在点 的关联点 ,则点 的坐标是 ;
(2)若在线段 上存在点 的关联点 ,求实数 的取值范围;
(3)分别以点 、 为圆心,1为半径作 、 .若对 上的任意一点 ,在 上总存在点 ,使得 、 两点互相关联,请写出点 的坐标.

如图, 、 、 、 是直线 上的四点, , , .
(1)求证: ;
(2)将 沿直线 翻折得到△ .
①用直尺和圆规在图中作出△ (保留作图痕迹,不要求写作法);
②连接 ,则直线 与 的位置关系是 .

如图,在 中, , , , 是 上一点(点 与点 不重合).若在 的直角边上存在4个不同的点分别和点 、 成为直角三角形的三个顶点,则 长的取值范围是 .

如图,在 中, , , 、 分别在 、 上,点 在 内.若四边形 是边长为1的正方形,则 .

中国古代数学家刘徽在《九章算术注》中,给出了证明三角形面积公式的出入相补法.如图所示,在 中,分别取 、 的中点 、 ,连接 ,过点 作 ,垂足为 ,将 分割后拼接成矩形 .若 , ,则 的面积是 .
