我们新定义一种三角形:两边平方和等于第三边平方的两倍的三角形叫做奇异三角形.
(1)根据“奇异三角形”的定义,请你判断命题“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt△ABC中,∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a:b:c;
(3)如图,AB是⊙O的直径,C是⊙O上一点(不与点A,B重合),D是半圆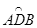 的中点,C,D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
的中点,C,D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.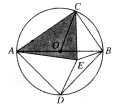
①求证:△ACE是奇异三角形;
②当△ACE是直角三角形时,求∠AOC的度数.
如图:OP平分∠MON,PA⊥ON于A,点Q是射线OM上的一个动点,若PA=2,则PQ的最小值为( ) 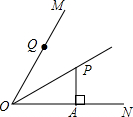
| A.1 | B.2 | C.3 | D.4 |
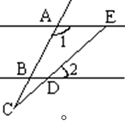
如图,AE‖BD,∠1=120°,∠2=40°,则∠C的度数是
| A.10°; | B.20°; |
| C.30°; | D.40° |
如图,将含30°角的直角三角尺ABC绕点B顺时针旋转 
150°后得到△EBD,连结CD.若AB="4cm." 则△BCD的面积
为( )
A.4 B.2 C.3 D.2
如图,点P是矩形ABCD的边AD的一个动点,矩形的
两条边AB、BC的长分别为3和4,那么点P到矩形的两条
对角线AC和BD的距离之和是__
(本题12分)已知两个全等的直角三角形纸片ABC、DEF,如图(1)放置,点B、D重合,点F在BC上,AB与EF交于点G,∠C=∠EFB=90°,∠E=∠ABC=30°,AB=DE=4.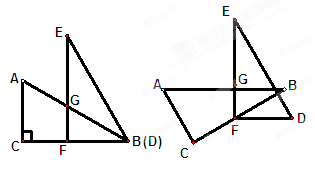
(1)求证:△EGB是等腰三角形
(2)若纸片DEF不动,问△ABC绕点F逆时针旋转最小 度时,四边形ACDE成为以ED为底的梯形(如图(2)),求此梯形的高。
如图8所示,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是( )
 图8
图8
| A.甲和乙 | B.乙和丙 | C.只有乙 | D.只有丙 |
如图7所示,在△ABC中,AB=AC,BE=CE,则由“SSS”可以判定( )
| A.△ABD≌△ACD | B.△BDE≌△CDE | C.△ABE≌△ACE | D.以上都不对 |

全等三角形是( )
| A.三个角对应相等的三角形 | B.周长相等的两个三角形 |
C.面 积相等的两个三角形 积相等的两个三角形 |
D.三边对应相等的两个三角形 |