初中数学三角形试题

如图，要在公路上增加一个公共汽车站，A、B是路边两个小区，这个公共汽车
站建在什么位置，使车站到小区的路程一样长？（尺规作图）

如图，OP平分∠ AOB，PD⊥ OA于点D，点Q是射线OB上一个动点，若PD=2，则PQ的最小值为（ ）

A．PQ＜2

B．PQ=2

C．PQ＞2

D．以上情况都有可能

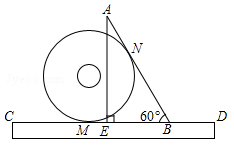
（年贵州省贵阳市）小明把半径为1的光盘、直尺和三角尺形状的纸片按如图所示放置于桌面上，此时，光盘与AB，CD分别相切于点N，M．现从如图所示的位置开始，将光盘在直尺边上沿着CD向右滚动到再次与AB相切时，光盘的圆心经过的距离是     ．

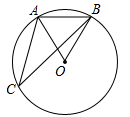
（年云南省）如图，点A，B，C是⊙O上的点，OA=AB，则∠C的度数为          ．

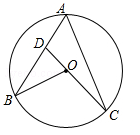
（年江西省南昌市）如图，点A，B，C在⊙O上，CO的延长线交AB于点D，∠A=50°，∠B=30°，则∠ADC的度数为            ．

（年贵州省黔东南州）如图，AD是⊙O的直径，弦BC⊥AD于E，AB=BC=12，则OC=       ．

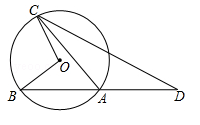
（年青海省中考）如图，点O为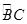所在圆的圆心，∠BOC=112°，点D在BA的延长线上，AD=AC，则∠D=          ．

（年贵州省遵义市）如图，在圆心角为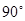的扇形OAB中，半径OA=2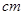，C为弧AB的中点，D，E分别是OA，OB的中点，则图中阴影部分的面积为         ．

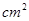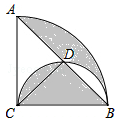
（年青海省西宁市）如图，在半径为2，圆心角为90°的扇形内，以BC为直径作半圆交AB于点D，连接CD，则阴影部分的面积是（ ）

A．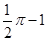

B．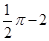

C．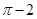

D．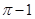

（年贵州省黔南州）如图，边长为1的菱形ABCD的两个顶点B、C恰好落在扇形AEF的弧EF上．若∠BAD=120°，则弧BC的长度等于     （结果保留π）．

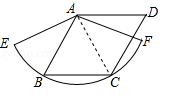
（年贵州省贵阳市）如图，⊙O是△ABC的外接圆，AB是⊙O的直径，FO⊥AB，垂足为点O，连接AF并延长交⊙O于点D，连接OD交BC于点E，∠B=30°，FO=．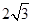

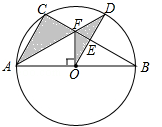
（1）求AC的长度；
（2）求图中阴影部分的面积．（计算结果保留根号）

（年贵州省毕节）如图，以△ABC的BC边上一点O为圆心的圆，经过A，B两点，且与BC边交于点E，D为BE的下半圆弧的中点，连接AD交BC于F，AC=FC．

（1）求证：AC是⊙O的切线；
（2）已知圆的半径R=5，EF=3，求DF的长．

（年云南省昆明市）如图，AH是⊙O的直径，AE平分∠FAH，交⊙O于点E，过点E的直线FG⊥AF，垂足为F，B为直径OH上一点，点E、F分别在矩形ABCD的边BC和CD上．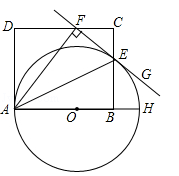

（1）求证：直线FG是⊙O的切线；
（2）若CD=10，EB=5，求⊙O的直径．

（年青海省中考）如图，在△ABC中，∠B=60°，⊙O是△ABC的外接圆，过点A作⊙O的切线，交CO的延长线于点M，CM交⊙O于点D．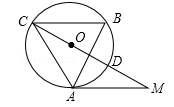

（1）求证：AM=AC；
（2）若AC=3，求MC的长．

（年新疆乌鲁木齐市）如图，AB是⊙O的直径，CD与⊙O相切于点C，与AB的延长线交于点D，DE⊥AD且与AC的延长线交于点E．

（1）求证：DC=DE；
（2）若tan∠CAB=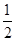，AB=3，求BD的长．