初中数学三角形试题

两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AD=CD，AB=CB，小明在探究筝形的性质时，得到如下结论：

①AC⊥BD；②AO=CO=AC；③△ABD≌△CBD，其中正确的结论有（  ）

A．①②

B．①③

C．②③

D．①②③

如图，已知AE=CF，∠AFD=∠CEB，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是（  ）

A．AD=CB

B．∠A=∠C

C．BE=DF

D．AD//BC

若三角形三个内角度数的比为1∶2∶3，则这个三角形的最小角是（  ）

A．30°

B．45°

C．60°

D．90°

已知三角形两边的长分别是4和10，则此三角形第三边的长可能是（  ）

A．5

B．6

C．11

D．16

如图，过△ABC的顶点A，作BC边上的高，以下作法正确的是（  ）

A．

B．

C．

D．

已知等腰三角形的两边长分别为6cm、3cm，则该等腰三角形的周长是（  ）

A．9cm

B．12cm

C．12cm或15cm

D．15cm

如图，已知△ABC≌△ADC，∠B=30°，∠DAC=25°，则∠ACB=（  ）

A．55°

B．60°

C．120°

D．125°

下列三角形中，不是直角三角形的是（  ）

A．△ABC中，∠C-∠B=∠A

B．△ABC中，a：b：c=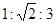

C．△ABC中，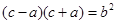

D．△ABC中，∠A：∠B：∠C=1：3：4

以下列各组线段为边，能组成三角形的是（  ）

A．2，3，5

B．3，3，6

C．2，5，8

D．4，5，6

如图．等边△ABC中，∠ABC与∠ACB的平分线相交于点O，且OD∥AB，OE∥AC．


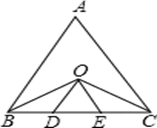
（1）试判定△ODE的形状．并说明你的理由；
（2）线段BD、DE、EC三者有什么关系？写出你的判断过程．

△ABC在平面直角坐标系xOy中的位置如图所示．

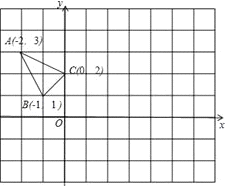
（1）作△ABC关于y轴成轴对称的△A₁B₁C₁；
（2）将△A₁B₁C₁向右平移4个单位，作出平移后的△A₂B₂C₂；则此三角形的面积为       ．
（3）在x轴上求作一点P，使PA₁+PC₂的值最小，点P的坐标为       ．

如图，在ΔABC与ΔDCB 中，AC与BD 交于点E，且，∠A=∠D，AB=DC．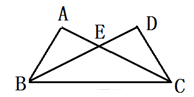

（1）求证：ΔABE≌ΔDCE
（2）当∠AEB=70°时，求∠EBC的度数．

如图，点D是△ABC的边BC上任意一点，点E、F分别是线段AD、CE的中点，且△ABC的面积为16cm²，则△BEF的面积：            cm²．

如图，AB=AC，要使△ABE≌△ACD，依据ASA，应添加的一个条件是          ．

如图，在△ABC中，∠ACB=90°，∠BAC=30°，在直线BC或AC上取一点P，使得△PAB为等腰三角形，这样的点P共有           个．