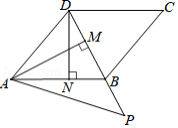
如图,在平行四边形 中,连接 ,且 ,过点 作 于点 ,过点 作 于点 ,且 ,在 的延长线上取一点 ,满足 ,则 .
有一架竖直靠在直角墙面的梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最小时扑捉.把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点,模型如图, ,点 , 分别在射线 , 上, 长度始终保持不变, , 为 的中点,点 到 , 的距离分别为4和2.在此滑动过程中,猫与老鼠的距离 的最小值为 .

如图,点 在直线 上,过点 作 轴交直线 于点 ,以点 为直角顶点, 为直角边在 的右侧作等腰直角△ ,再过点 作 轴,分别交直线 和 于 , 两点,以点 为直角顶点, 为直角边在 的右侧作等腰直角△ ,按此规律进行下去,则等腰直角△ 的面积为 .(用含正整数 的代数式表示)

如图,两个大小不同的三角板放在同一平面内,直角顶点重合于点,点
在
上,
,
与
交于点
,连接
,若
,
,则
.

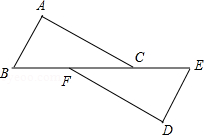
如图,在 和 中,点 , , , 在同一直线上, , ,请添加一个条件,使 ,这个添加的条件可以是 (只需写一个,不添加辅助线).
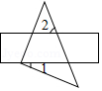
把一块含有角的直角三角板与两条长边平行的直尺如图放置(直角顶点在直尺的一条长边上).若
,则
.
已知直线,将一块含
角的直角三角板
按如图所示方式放置
,并且顶点
,
分别落在直线
,
上,若
,则
的度数是 .

如图,已知线段 , 是 的中点,直线 经过点 , , 点是直线 上一点,当 为直角三角形时,则 .

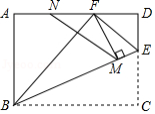
如图,矩形纸片 , , , 为边 上一点.将 沿 所在的直线折叠,点 恰好落在 边上的点 处,过点 作 ,垂足为点 ,取 的中点 ,连接 ,则 .
如图,将面积为 的矩形 沿对角线 折叠,点 的对应点为点 ,连接 交 于点 .若 ,则 的长为 .
