(1)如图1,在中,
,以点
为中心,把
逆时针旋转
,得到△
;再以点
为中心,把
顺时针旋转
,得到△
,连接
,则
与
的位置关系为 ;
(2)如图2,当是锐角三角形,
时,将
按照(1)中的方式旋转
,连接
,探究
与
的位置关系,写出你的探究结论,并加以证明;
(3)如图3,在图2的基础上,连接,若
,△
的面积为4,则△
的面积为 .

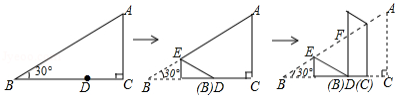
在三角形纸片中,
,
,点
(不与
,
重合)是
上任意一点,将此三角形纸片按下列方式折叠,若
的长度为
,则
的周长为 (用含
的式子表示).
如图,已知线段,分别以点
和点
为圆心,大于
的长为半径作弧,两弧相交于
、
两点,作直线
交
于点
,在直线
上任取一点
,连接
,
.若
,则
.

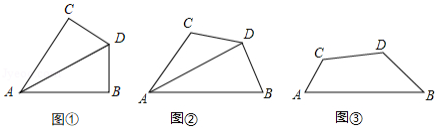
感知:如图1,平分
.
,
,易知:
.
探究:如图2,平分
,
,
,求证:
.
应用:如图3,四边形中,
,
,
,则
(用含
的代数式表示)
如图,在中,
,按以下步骤作图:分别以点
和点
为圆心,大于
一半的长为半径作圆弧,两弧相交于点
和点
,作直线
交
于点
;连结
.若
,
,则
的周长为 .
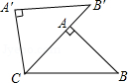
如图,在 中, ,将 绕点 按逆时针方向旋转 得到 △ ,点 在边 上,则 的大小为
| A. |
|
B. |
|
C. |
|
D. |
|
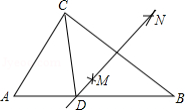
如图,点为
中点,分别延长
到点
,
到点
,使
.以点
为圆心,分别以
,
为半径在
上方作两个半圆.点
为小半圆上任一点(不与点
,
重合),连接
并延长交大半圆于点
,连接
,
.
(1)①求证:;
②写出,
和
三者间的数量关系,并说明理由.
(2)若,当
最大时,直接指出
与小半圆的位置关系,并求此时
(答案保留
.
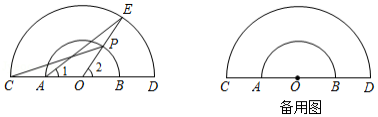
如图是用三块正方形纸片以顶点相连的方式设计的"毕达哥拉斯"图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是

| A. |
1,4,5 |
B. |
2,3,5 |
C. |
3,4,5 |
D. |
2,2,4 |
如图,从笔直的公路 旁一点 出发,向西走 到达 ;从 出发向北走 也到达 .下列说法错误的是

| A. |
从点 向北偏西 走 到达 |
| B. |
公路 的走向是南偏西 |
| C. |
公路 的走向是北偏东 |
| D. |
从点 向北走 后,再向西走 到达 |
如图,和
中,
,
,
,边
与边
交于点
(不与点
,
重合),点
,
在
异侧,
为
的内心.
(1)求证:;
(2)设,请用含
的式子表示
,并求
的最大值;
(3)当时,
的取值范围为
,分别直接写出
,
的值.

已知:整式,整式
.
尝试 化简整式.
发现,求整式
.
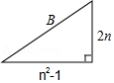
联想 由上可知,,当
时,
,
,
为直角三角形的三边长,如图.填写下表中
的值:
直角三角形三边 |
|||
勾股数组Ⅰ |
8 |
17 |
|
勾股数组Ⅱ |
35 |
|
勘测队按实际需要构建了平面直角坐标系,并标示了,
,
三地的坐标,数据如图(单位:
.笔直铁路经过
,
两地.
(1),
间的距离为
;
(2)计划修一条从到铁路
的最短公路
,并在
上建一个维修站
,使
到
,
的距离相等,则
,
间的距离为
.

下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容

则回答正确的是
| A. |
◎代表 |
B. |
代表同位角 |
C. |
▲代表 |
D. |
※代表 |