如图,在 中,已知 .
(1)实践与操作:作 的平分线交 于点 ,在 上截取 ,连接 ;(要求:尺规作图,保留作图痕迹,不写作法)
(2)猜想并证明:猜想四边形 的形状,并给予证明.

如图,在中,
,
,
.
(1)尺规作图:不写作法,保留作图痕迹.
①作的平分线,交斜边
于点
;
②过点作
的垂线,垂足为点
.
(2)在(1)作出的图形中,求的长.

如图,已知A、O、B三点在同一条直线上,
平分
,
平分
.

(1)若
,求
的度数;
(2)若
,求
的度数;
(3)图中是否有互余的角?若有请写出所有互余的角.
问题引入:
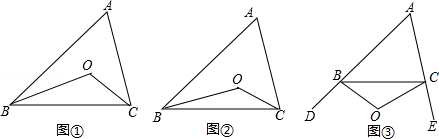
(1)如图①,在 中,点 是 和 平分线的交点,若 ,则 (用 表示);如图②, , , ,则 (用 表示)
拓展研究:
(2)如图③, , , ,请猜想 (用 表示),并说明理由.
类比研究:
(3) 、 分别是 的外角 、 的 等分线,它们交于点 , , , ,请猜想 .
如图,在 中, ,点 是斜边 上一点,且 .
(1)作 的平分线,交 于点 ;(要求尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,连接 ,求证: .

如图,已知
与
互为余角,且
,
平分
,
平分
.

(1)求
的度数;
(2)如果已知中
,其他条件不变,求
的度数;
(3)如果已知中
,其他条件不变,求
的度数;
(4)从(1)、(2)、(3)中你能看出有什么规律.
如图, 是 的角平分线,在 上取点 ,使 .
(1)求证: ;
(2)若 , ,求 的度数.

如图,直线AB、CD、EF相交于点O,OG⊥CD,∠BOD=32°.
(1)求∠AOG的度数;
(2)如果OC是∠AOE的平分线,那么OG是∠AOF的平分线吗?请说明理由.
如图,在 中,以点 为圆心, 长为半径画弧交 于点 ,再分别以点 、 为圆心,大于 的相同长为半径画弧,两弧交于点 ;连接 并延长交 于点 ,连接 ,则所得四边形 是菱形.
(1)根据以上尺规作图的过程,求证:四边形 是菱形;
(2)若菱形 的周长为16, ,求 的大小.

如图,在中,
是
边上的一点,
,
平分
,交
边于点
,连接
.
(1)求证:;
(2)若,
,求
的度数.

如图,已知直线AB和CD相交于O点,∠COE=90°,OF平分∠AOE,∠COF=28°,求∠BOD的度数.