初中数学角平分线的定义解答题

如图．等边△ABC中，∠ABC与∠ACB的平分线相交于点O，且OD∥AB，OE∥AC．


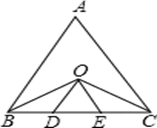
（1）试判定△ODE的形状．并说明你的理由；
（2）线段BD、DE、EC三者有什么关系？写出你的判断过程．

如图，与是邻补角，OD、OE分别是与的平分线，试判断OD与OE的位置关系，并说明理由．

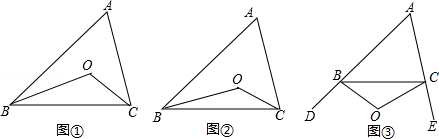
已知如图（1）：△ABC中，AB=AC，∠B、∠C的平分线相交于点O，过点O作EF∥BC分别交AB、AC于E、F．

（1）写出线段EF与BE、CF间的数量关系？（不证明）
（2）若AB≠AC，其他条件不变，如图（2），图中线段EF与BE、CF间是否存在（1）中数量关系？请说明理由．
（3）若△ABC中，AB≠AC，∠B的平分线与三角形外角∠ACD的平分线CO交于O，过O点作OE∥BC交AB于E，交AC于F，如图（3），这时图中线段EF与BE，CF间存在什么数量关系？请说明理由．

如图，O是直线AB上一点，OD平分∠BOC，∠COE=90°．若∠AOC=40°，求∠DOE的度数．

问题引入：

（1）如图①，在 $\mathit{\Delta ABC}$中，点 $O$是 $\angle \mathit{ABC}$和 $\angle \mathit{ACB}$平分线的交点，若 $\angle A=\alpha$，则 $\angle \mathit{BOC}=$　　（用 $\alpha$表示）；如图②， $\angle \mathit{CBO}=\frac{1}{3}\angle \mathit{ABC}$， $\angle \mathit{BCO}=\frac{1}{3}\angle \mathit{ACB}$， $\angle A=\alpha$，则 $\angle \mathit{BOC}=$　　（用 $\alpha$表示）

拓展研究：

（2）如图③， $\angle \mathit{CBO}=\frac{1}{3}\angle \mathit{DBC}$， $\angle \mathit{BCO}=\frac{1}{3}\angle \mathit{ECB}$， $\angle A=\alpha$，请猜想 $\angle \mathit{BOC}=$　　（用 $\alpha$表示），并说明理由．

类比研究：

（3） $\mathit{BO}$、 $\mathit{CO}$分别是 $\mathit{\Delta ABC}$的外角 $\angle \mathit{DBC}$、 $\angle \mathit{ECB}$的 $n$等分线，它们交于点 $O$， $\angle \mathit{CBO}=\frac{1}{n}\angle \mathit{DBC}$， $\angle \mathit{BCO}=\frac{1}{n}\angle \mathit{ECB}$， $\angle A=\alpha$，请猜想 $\angle \mathit{BOC}=$　　．

如图，在中，，，．

（1）尺规作图：不写作法，保留作图痕迹．

①作的平分线，交斜边于点；

②过点作的垂线，垂足为点．

（2）在（1）作出的图形中，求的长．

如图，直线，平分，，求的度数．

如图，，点是上一点，，平分交于点，求的度数．

如图，在 $\text{Rt}\Delta \text{ABC}$ 中， $\angle \mathit{ACB}=90°$ ，点 $D$ 是斜边 $\mathit{AB}$ 上一点，且 $\mathit{AC}=\mathit{AD}$ ．

（1）作 $\angle \mathit{BAC}$ 的平分线，交 $\mathit{BC}$ 于点 $E$ ；（要求尺规作图，不写作法，保留作图痕迹）

（2）在（1）的条件下，连接 $\mathit{DE}$ ，求证： $\mathit{DE}\perp \mathit{AB}$ ．

如图，在 $▱\mathit{ABCD}$中，已知 $\mathit{AD}>\mathit{AB}$．

（1）实践与操作：作 $\angle \mathit{BAD}$的平分线交 $\mathit{BC}$于点 $E$，在 $\mathit{AD}$上截取 $\mathit{AF}=\mathit{AB}$，连接 $\mathit{EF}$；（要求：尺规作图，保留作图痕迹，不写作法）

（2）猜想并证明：猜想四边形 $\mathit{ABEF}$的形状，并给予证明．

如图，已知平分，．求证：．

如图，已知 $\angle AOM$ 与 $\angle MOB$ 互为余角，且 $\angle BOC=30°$ ， $OM$ 平分 $\angle AOC$ ， $ON$ 平分 $\angle BOC$ ．

（1）求 $\angle MON$ 的度数；
（2）如果已知中 $\angle AOB=80°$ ，其他条件不变，求 $\angle MON$ 的度数；
（3）如果已知中 $\angle BOC=60°$ ，其他条件不变，求 $\angle MON$ 的度数；
（4）从（1）、（2）、（3）中你能看出有什么规律．

如图直线 $\mathit{EF}$ 分别与直线 $\mathit{AB}$ ， $\mathit{CD}$ 交于点 $E$ ， $F$ ． $\mathit{EM}$ 平分 $\angle \mathit{BEF}$ ， $\mathit{FN}$ 平分 $\angle \mathit{CFE}$ ，且 $\mathit{EM}//\mathit{FN}$ ．求证： $\mathit{AB}//\mathit{CD}$ ．

如图，已知A、O、B三点在同一条直线上， $OD$ 平分 $\angle AOC$ ， $OE$ 平分 $\angle BOC$ ．

（1）若 $\angle BOC=62°$ ，求 $\angle DOE$ 的度数；
（2）若 $\angle BOC=a°$ ，求 $\angle DOE$ 的度数；
（3）图中是否有互余的角？若有请写出所有互余的角．

如图， $\mathit{BE}$ 是 $\mathit{\Delta ABC}$ 的角平分线，在 $\mathit{AB}$ 上取点 $D$ ，使 $\mathit{DB}=\mathit{DE}$ ．

（1）求证： $\mathit{DE}//\mathit{BC}$ ；

（2）若 $\angle A=65°$ ， $\angle \mathit{AED}=45°$ ，求 $\angle \mathit{EBC}$ 的度数．