如图,在平面直角坐标系中,四边形 的边 在 轴上,点 在 轴的负半轴上,直线 ,且 , ,将经过 、 两点的直线 向右平移,平移后的直线与 轴交于点 ,与直线 交于点 ,设 的长为 .
(1)四边形 的面积为 ;
(2)设四边形 被直线 扫过的面积(阴影部分)为 ,请直接写出 关于 的函数解析式;
(3)当 时,直线 上有一动点 ,作 直线 于点 ,交 轴于点 ,将 沿直线 折叠得到 ,探究:是否存在点 ,使点 恰好落在坐标轴上?若存在,请求出点 的坐标;若不存在,请说明理由.

如图,在直角坐标系 中,菱形 的边 在 轴正半轴上,点 , 在第一象限, ,边长 .点 从原点 出发沿 轴正半轴以每秒1个单位长的速度作匀速运动,点 从 出发沿边 以每秒2个单位长的速度作匀速运动,过点 作直线 垂直于 轴并交折线 于 ,交对角线 于 ,点 和点 同时出发,分别沿各自路线运动,点 运动到原点 时, 和 两点同时停止运动.
(1)当 时,求线段 的长;
(2)求 为何值时,点 与 重合;
(3)设 的面积为 ,求 与 的函数关系式及 的取值范围.

某农作物的生长率与温度
有如下关系:如图1,当
时可近似用函数
刻画;当
时可近似用函数
刻画.
(1)求的值.
(2)按照经验,该作物提前上市的天数(天
与生长率
满足函数关系:
生长率 |
0.2 |
0.25 |
0.3 |
0.35 |
提前上市的天数 |
0 |
5 |
10 |
15 |
①请运用已学的知识,求关于
的函数表达式;
②请用含的代数式表示
.
(3)天气寒冷,大棚加温可改变农作物生长速度.在(2)的条件下,原计划大棚恒温时,每天的成本为200元,该作物30天后上市时,根据市场调查:每提前一天上市售出(一次售完),销售额可增加600元.因此给大棚继续加温,加温后每天成本
(元
与大棚温度
之间的关系如图2.问提前上市多少天时增加的利润最大?并求这个最大利润(农作物上市售出后大棚暂停使用).
已知:如图,在平面直角坐标系中,点 , ,过点 的直线 与 轴正半轴交于点 ,与直线 交于点 .
(1)当 且 时,求 的长度;
(2)若点 的坐标是 ,且 ,求经过点 且以点 为顶点的抛物线的函数表达式.

如图,矩形 中, 是 的中点,将 沿 翻折,点 落在点 处, .设 , 的面积为 ,则 与 的函数图象大致为

A. B.
B.
C.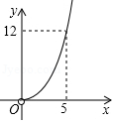 D.
D.
如图所示,已知 中, , 边上的高 , 为 上一点, ,交 于点 ,交 于点 ,设点 到边 的距离为 .则 的面积 关于 的函数图象大致为

A. B.
B.
C. D.
D.
如图,以原点 为圆心,3为半径的圆与 轴分别交于 , 两点(点 在点 的右边), 是半径 上一点,过 且垂直于 的直线与 分别交于 , 两点(点 在点 的上方),直线 , 交于点 .若 .
(1)求点 的坐标;
(2)求过点 和点 ,且顶点在直线 上的抛物线的函数表达式.

如图,在矩形 中, ,点 在边 上,连接 ,以 为边向右上方作正方形 ,作 ,垂足为 ,连接 .
(1)求证: ;
(2)当 为何值时, 的面积最大?
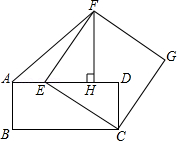
如图,正方形 的顶点在边长为2的正方形的边上.若设 ,正方形 的面积为 ,则 与 的函数关系为 .

2020年新冠肺炎疫情期间,部分药店趁机将口罩涨价,经调查发现某药店某月(按30天计)前5天的某型号口罩销售价格 (元 只)和销量 (只 与第 天的关系如下表:
| 第 天 |
1 |
2 |
3 |
4 |
5 |
| 销售价格 (元 只) |
2 |
3 |
4 |
5 |
6 |
| 销量 (只 |
70 |
75 |
80 |
85 |
90 |
物价部门发现这种乱象后,统一规定各药店该型号口罩的销售价格不得高于1元 只,该药店从第6天起将该型号口罩的价格调整为1元 只.据统计,该药店从第6天起销量 (只 与第 天的关系为 ,且 为整数),已知该型号口罩的进货价格为0.5元 只.
(1)直接写出该药店该月前5天的销售价格 与 和销量 与 之间的函数关系式;
(2)求该药店该月销售该型号口罩获得的利润 (元 与 的函数关系式,并判断第几天的利润最大;
(3)物价部门为了进一步加强市场整顿,对此药店在这个月销售该型号口罩的过程中获得的正常利润之外的非法所得部分处以 倍的罚款,若罚款金额不低于2000元,则 的取值范围为 .
某农作物的生长率与温度
有如下关系:如图,当
时可近似用函数
刻画;当
时可近似用函数
刻画.
(1)求的值.
(2)按照经验,该作物提前上市的天数(天
与生长率
之间满足已学过的函数关系,部分数据如下:
生长率 |
0.2 |
0.25 |
0.3 |
0.35 |
提前上市的天数 |
0 |
5 |
10 |
15 |
求:①关于
的函数表达式;
②用含的代数式表示
.
③天气寒冷,大棚加温可改变农作物生长速度.大棚恒温时每天的成本为100元,计划该作物30天后上市,现根据市场调查:每提前一天上市售出(一次售完),销售额可增加600元.因此决定给大棚继续加温,但加温导致成本增加,估测加温到
时的成本为200元
天,但若欲加温到
,由于要采用特殊方法,成本增加到400元
天.问加温到多少度时增加的利润最大?并说明理由.(注
农作物上市售出后大棚暂停使用)

某宾馆有若干间标准房,当标准房的价格为200元时,每天入住的房间数为60间.经市场调查表明,该馆每间标准房的价格在元之间(含170元,240元)浮动时,每天入住的房间数
(间
与每间标准房的价格
(元
的数据如下表:
|
190 |
200 |
210 |
220 |
||
|
65 |
60 |
55 |
50 |
(1)根据所给数据在坐标系中描出相应的点,并画出图象.
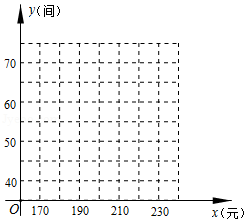
(2)求关于
的函数表达式,并写出自变量
的取值范围.
(3)设客房的日营业额为(元
.若不考虑其他因素,问宾馆标准房的价格定为多少元时,客房的日营业额最大?最大为多少元?
如图,点 、 、 、 是正方形 四条边(不含端点)上的点, 设线段 的长为 ,四边形 的面积为 ,则能够反映 与 之间函数关系的图象大致是

| A. |
|
B. |
|
| C. |
|
D. |
|
如图,在 中, , , ,点 是 边上的动点(不与点 重合),过 作 ,垂足为 ,点 是 的中点,连接 ,设 , 的面积为 ,则 与 之间的函数关系式为 .
