北中环桥是省城太原的一座跨汾河大桥(如图 ,它由五个高度不同,跨径也不同的抛物线型钢拱通过吊桥,拉索与主梁相连,最高的钢拱如图2所示,此钢拱(近似看成二次函数的图象 抛物线)在同一竖直平面内,与拱脚所在的水平面相交于 , 两点.拱高为78米(即最高点 到 的距离为78米),跨径为90米(即 米),以最高点 为坐标原点,以平行于 的直线为 轴建立平面直角坐标系,则此抛物线钢拱的函数表达式为
| A. |
|
B. |
|
C. |
|
D. |
|
相关知识点
推荐套卷
 的解为坐标的点
的解为坐标的点 在平面直角坐标系中的位置是 ( )
在平面直角坐标系中的位置是 ( ) 中,对角线
中,对角线 分别等于8和6,将
分别等于8和6,将 沿
沿 的方向平移,使
的方向平移,使 与
与 重合,
重合, 与
与 重合,则四边形
重合,则四边形 的面积等于( )
的面积等于( )


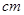
 粤公网安备 44130202000953号
粤公网安备 44130202000953号