初中数学反比例函数的性质试题

如图，已知反比例函数 $y=\frac{k_1}{x}(x>0)$的图象与反比例函数 $y=\frac{k_2}{x}(x<0)$的图象关于 $y$轴对称， $A(1,4)$， $B(4,m)$是函数 $y=\frac{k_1}{x}(x>0)$图象上的两点，连接 $\mathit{AB}$，点 $C(-2,n)$是函数 $y=\frac{k_2}{x}(x<0)$图象上的一点，连接 $\mathit{AC}$， $\mathit{BC}$．

（1）求 $m$， $n$的值；

（2）求 $\mathit{AB}$所在直线的表达式；

（3）求 $\mathit{\Delta ABC}$的面积．

在反比例函数 $y=-\frac{2}{x}$图象上有三个点 $A(x_1$， $y_1)$、 $B(x_2$， $y_2)$、 $C(x_3$， $y_3)$，若 $x_1<0<x_2<x_3$，则下列结论正确的是 $($　　 $)$

A． $y_3<y_2<y_1$B． $y_1<y_3<y_2$C． $y_2<y_3<y_1$D． $y_3<y_1<y_2$

给出下列函数：① $y=-3x+2$；② $y=\frac{3}{x}$；③ $y=2x^2$；④ $y=3x$，上述函数中符合条件“当 $x>1$时，函数值 $y$随自变量 $x$增大而增大“的是 $($　　 $)$

A．①③B．③④C．②④D．②③

若点 $A(-2,y_1)$、 $B(-1,y_2)$、 $C(1,y_3)$都在反比例函数 $y=\frac{k^2-2k+3}{x}(k$为常数）的图象上，则 $y_1$、 $y_2$、 $y_3$的大小关系为　 $y_2<y_1<y_3$　．

如图，在平面直角坐标系中，经过点 $A$的双曲线 $y=\frac{k}{x}(x>0)$同时经过点 $B$，且点 $A$在点 $B$的左侧，点 $A$的横坐标为 $\sqrt{2}$， $\angle \mathit{AOB}=\angle \mathit{OBA}=45°$，则 $k$的值为　　．

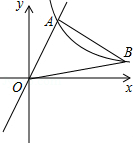
如图，分别位于反比例函数 $y=\frac{1}{x}$， $y=\frac{k}{x}$在第一象限图象上的两点 $A$、 $B$，与原点 $O$在同一直线上，且 $\frac{\mathit{OA}}{\mathit{OB}}=\frac{1}{3}$．

（1）求反比例函数 $y=\frac{k}{x}$的表达式；

（2）过点 $A$作 $x$轴的平行线交 $y=\frac{k}{x}$的图象于点 $C$，连接 $\mathit{BC}$，求 $\mathit{\Delta ABC}$的面积．

请写出一个过点 $(1,1)$，且与 $x$轴无交点的函数解析式：　　．

如图1， $▱\mathit{OABC}$的边 $\mathit{OC}$在 $y$轴的正半轴上， $\mathit{OC}=3$， $A(2,1)$，反比例函数 $y=\frac{k}{x}(x>0)$的图象经过的 $B$．

（1）求点 $B$的坐标和反比例函数的关系式；

（2）如图2，直线 $\mathit{MN}$分别与 $x$轴、 $y$轴的正半轴交于 $M$， $N$两点，若点 $O$和点 $B$关于直线 $\mathit{MN}$成轴对称，求线段 $\mathit{ON}$的长；

（3）如图3，将线段 $\mathit{OA}$延长交 $y=\frac{k}{x}(x>0)$的图象于点 $D$，过 $B$， $D$的直线分别交 $x$轴、 $y$轴于 $E$， $F$两点，请探究线段 $\mathit{ED}$与 $\mathit{BF}$的数量关系，并说明理由．

如图，一次函数 $y=\mathit{kx}+b$与反比例函数 $y=\frac{a}{x}$的图象在第一象限交于 $A$、 $B$两点， $B$点的坐标为 $(3,2)$，连接 $\mathit{OA}$、 $\mathit{OB}$，过 $B$作 $\mathit{BD}\perp y$轴，垂足为 $D$，交 $\mathit{OA}$于 $C$，若 $\mathit{OC}=\mathit{CA}$．

（1）求一次函数和反比例函数的表达式；

（2）求 $\mathit{\Delta AOB}$的面积．

下列函数中，对于任意实数 $x_1$， $x_2$，当 $x_1>x_2$时，满足 $y_1<y_2$的是 $($　　 $)$

A． $y=-3x+2$B． $y=2x+1$

C． $y=2x^2+1$D． $y=-\frac{1}{x}$

反比例函数 $y=\frac{6}{x}$的图象上有两点 $(-2$， $y_1\left)\right(1$， $y_2)$，那么 $y_1$与 $y_2$的关系为 $($　　 $)$

A． $y_1>y_2$B． $y_1=y_2$C． $y_1<y_2$D．不能确定

如图，一次函数 $y=\mathit{kx}+2$的图象与反比例函数 $y=\frac{m}{x}(x<0)$的图象在第二象限交于点 $P$，过点 $P$作 $\mathit{PA}\perp x$轴于点 $A$，一次函数的图象分别交 $x$、 $y$轴于点 $C$、 $B$， $S_{\mathit{\Delta OBC}}=1$， $\mathit{OA}=\mathit{OC}$

（1）求点 $B$的坐标；

（2）求一次函数与反比例函数的表达式；

（3）根据图象直接写出不等式 $\mathit{kx}+2>\frac{m}{x}$的解集．

反比例函数 $y=\frac{a}{x}(a>0$， $a$为常数）和 $y=\frac{2}{x}$在第一象限内的图象如图所示，点 $M$在 $y=\frac{a}{x}$的图象上， $\mathit{MC}\perp x$轴于点 $C$，交 $y=\frac{2}{x}$的图象于点 $A$； $\mathit{MD}\perp y$轴于点 $D$，交 $y=\frac{2}{x}$的图象于点 $B$，当点 $M$在 $y=\frac{a}{x}$的图象上运动时，以下结论：

① $S_{\mathit{\Delta ODB}}=S_{\mathit{\Delta OCA}}$；

②四边形 $\mathit{OAMB}$的面积不变；

③当点 $A$是 $\mathit{MC}$的中点时，则点 $B$是 $\mathit{MD}$的中点．

其中正确结论的个数是 $($　　 $)$

A．0B．1C．2D．3

已知反比例函数 $y=\frac{k}{x}(k\ne 0)$的图象经过 $(3,-1)$，则当 $1<y<3$时，自变量 $x$的取值范围是　              　．

如图，反比例函数 $y=\frac{m}{x}$的图象与一次函数 $y=\mathit{kx}+b$的图象交于 $A$， $B$两点，点 $A$的坐标为 $(2,6)$，点 $B$的坐标为 $(n,1)$．

（1）求反比例函数与一次函数的表达式；

（2）点 $E$为 $y$轴上一个动点，若 $S_{\mathit{\Delta AEB}}=5$，求点 $E$的坐标．