如图,正方形 的顶点 , 在函数 的图象上,点 , 分别在 轴, 轴的正半轴上,当 的值改变时,正方形 的大小也随之改变.
(1)当 时,正方形 的边长等于 .
(2)当变化的正方形 与(1)中的正方形 有重叠部分时, 的取值范围是 .
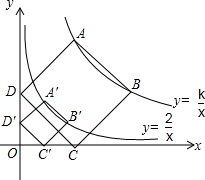
如图,点 为函数 图象上一点,连接 ,交函数 的图象于点 ,点 是 轴上一点,且 ,则 的面积为 .

如图,已知直线 ,双曲线 ,在 上取一点 , ,过 作 轴的垂线交双曲线于点 ,过 作 轴的垂线交 于点 ,过 作 轴的垂线交双曲线于点 ,过 作 轴的垂线交 于点 ,此时 与 重合,并得到一个正方形 ,若原点 在正方形 的对角线上且分这条对角线为 的两条线段,则 的值为 .
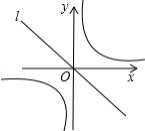
如图,曲线 是双曲线 绕原点 逆时针旋转 得到的图形, 是曲线 上任意一点,点 在直线 上,且 ,则 的面积等于

A. B.6C.3D.12
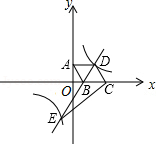
如图所示,四边形 是菱形,边 在 轴上,点 ,点 ,双曲线 与直线 交于点 、点 .
(1)求 的值;
(2)求直线 的解析式;
(3)求 的面积.
【探究函数 y = x + 4 x 的图象与性质】
(1)函数 的自变量 的取值范围是 ;
(2)下列四个函数图象中函数 的图象大致是 ;

(3)对于函数 ,求当 时, 的取值范围.
请将下列的求解过程补充完整.
解:
.
拓展运用
(4)若函数 ,则 的取值范围 .
若点 , , 在反比例函数 为常数)的图象上,则 , , 大小关系为
A. B. C. D.
如图,直线 为常数, 与双曲线 为常数, 的交点为 、 , 轴于点 , , .
(1)求 的值;
(2)点 在 轴上,如果 ,求 点的坐标.

如图,设反比例函数的解析式为 .
(1)若该反比例函数与正比例函数 的图象有一个交点的纵坐标为2,求 的值;
(2)若该反比例函数与过点 的直线 的图象交于 , 两点,如图所示,当 的面积为 时,求直线 的解析式.

如图,直线 与双曲线 交于点 , ,点 是直线 上一动点,且点 在第二象限.连接 并延长交双曲线于点 .过点 作 轴,垂足为点 .过点 作 轴,垂足为 .若点 的坐标为 ,点 的坐标为 ,设 的面积为 , 的面积为 ,当 时,点 的横坐标 的取值范围为 .
