初中数学反比例函数的性质试题

如图，在平面直角坐标系中，点 $P(1,4)$ 、 $Q(m,n)$ 在函数 $y=\frac{k}{x}(x>0)$ 的图象上，当 $m>1$ 时，过点 $P$ 分别作 $x$ 轴、 $y$ 轴的垂线，垂足为点 $A$ ， $B$ ；过点 $Q$ 分别作 $x$ 轴、 $y$ 轴的垂线，垂足为点 $C$ 、 $D$ ． $\mathit{QD}$ 交 $\mathit{PA}$ 于点 $E$ ，随着 $m$ 的增大，四边形 $\mathit{ACQE}$ 的面积 $($ 　　 $)$

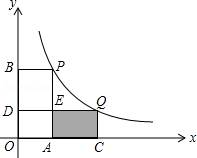
A．

减小

B．

增大

C．

先减小后增大

D．

先增大后减小

如图，函数 $y=\left\{\begin{array}{c}\frac{1}{x}(x>0),\\ -\frac{1}{x}(x<0)\end{array}\right.$ 的图象所在坐标系的原点是 $($ 　　 $)$

A．

点 $M$

B．

点 $N$

C．

点 $P$

D．

点 $Q$

如图，在平面直角坐标系中，函数的图象与直线交于点．

（1）求、的值；

（2）已知点，，过点作平行于轴的直线，交直线于点，过点作平行于轴的直线，交函数的图象于点．

①当时，判断线段与的数量关系，并说明理由；

②若，结合函数的图象，直接写出的取值范围．

如图，直线 $l\perp x$ 轴于点 $P$ ，且与反比例函数 $y_1=\frac{k_1}{x}(x>0)$ 及 $y_2=\frac{k_2}{x}(x>0)$ 的图象分别交于点 $A$ ， $B$ ，连接 $\mathit{OA}$ ， $\mathit{OB}$ ，已知 $\mathit{\Delta OAB}$ 的面积为2，则 $k_1-k_2=$ 　　．

已知抛物线 $y=a{x}^2+\mathit{bx}+c$ 与反比例函数 $y=\frac{b}{x}$ 的图象在第一象限有一个公共点，其横坐标为1，则一次函数 $y=\mathit{bx}+\mathit{ac}$ 的图象可能是 $($ 　　 $)$

A．

B．

C．

D．

如图，在x轴的上方，直角∠BOA绕原点O按顺时针方向旋转，若∠BOA的两边分别与函数y=﹣、y=的图象交于B、A两点，则∠OAB的大小的变化趋势为（  ）

A．逐渐变小       B．逐渐变大       C．无法确定       D．保持不变

如图，一次函数的图象与反比例函数的图象交于点P，点P在第一象限．PA⊥x轴于点A，PB⊥y轴于点B．一次函数的图象分别交轴、轴于点C、D，且S_△PBD=4，．

（1）求点D的坐标;
（2）求一次函数与反比例函数的解析式；
（3）根据图象写出当时，一次函数的值大于反比例函数的值的的取值范围．

已知点A（-2，y₁）、B（-1，y₂）、C（3，y₃）都在反比例函数y=的图象上，则（  ）

A．y1＜y2＜y3

B．y3＜y2＜y1

C．y3＜y1＜y2

D．y2＜y1＜y3

（年新疆、生产建设兵团）若点P₁（﹣1，m），P₂（﹣2，n）在反比例函数（）的图象上，则m      n．（填“＞”，“＜”或“=”）

（年贵州省遵义市）已知点A（-2，），B（3，）是反比例函数（）图象上的两点，则有（   ）．

A．

B．

C．

D．

在－1，1，2这三个数中任选2个数分别作为P点的横坐标和纵坐标，过P点画双曲线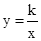，该双曲线位于第二、四象限的概率是        。

如图，点B₁在反比例函数y=（x＞0）的图象上，过点B₁分别作x轴和y轴的垂线，垂足为C₁和A，得到第一个矩形AOC₁B₁，点C₁的坐标为（1，0）；取x轴上一点C₂（，0），过点C₂作x轴的垂线交反比例函数图象于点B₂，过B₂作线段B₂ A₁⊥B₁C_1，，交B₁C₁于点A₁，得到第二个矩形A₁C₁C₂B₂；依次在x轴上取点C₃（2，0），C₄（，0） 按此规律作矩形，则第10个矩形A₉C₉C₁₀B₁₀的面积为     ．

设a、b是任意两个不等实数，我们规定：满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间，表示为[a，b]．对于一个函数，如果它的自变量x与函数值y满足：当m≤x≤n时，有m≤y≤n，我们就称此函数是闭区间[m，n]上的“闭函数”．
（1）反比例函数是闭区间[1，2014]上的“闭函数”吗？请判断并说明理由；
（2）若一次函数是闭区间[m，n]上的“闭函数”，求此函数的解析式；
（3）若二次函数是闭区间[a，b]上的“闭函数”，求实数a，b的值．

（2014年山东青岛3分）函数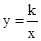与y=﹣kx²+k（k≠0）在同一直角坐标系中的图象可能是（   ）

A．

B．

C．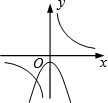

D．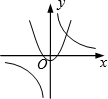

（2014年江西省3分）已知反比例函数的图像如图所示，则二次函数的图像大致为（   ）

A．

B．

C．

D．