专题13 函数之一次函数、反比例函数和二次函数综合问题(压轴题)
(2014年广西北海3分)函数y=ax2+1与 (a≠0)在同一平面直角坐标系中的图象可能是( )
(a≠0)在同一平面直角坐标系中的图象可能是( )
A. |
B. |
C. |
D. |
(2014年湖北宜昌3分)二次函数 (b>0)与反比例函数
(b>0)与反比例函数 在同一坐标系中的图象可能是( )
在同一坐标系中的图象可能是( )
A. |
B. |
C. |
D. |
(2014年湖南长沙3分)函数 与y=ax2(a≠0)在同一平面直角坐标系中的图象可能是( )
与y=ax2(a≠0)在同一平面直角坐标系中的图象可能是( )
A. |
B. |
C. |
D. |
(2014年江西省南昌3分)已知反比例函数 的图像如图所示,则二次函数
的图像如图所示,则二次函数 的图像大致为( )
的图像大致为( )

A. |
B. |
C. |
D. |
(2014年江西省3分)已知反比例函数 的图像如图所示,则二次函数
的图像如图所示,则二次函数 的图像大致为( )
的图像大致为( )

A. |
B. |
C. |
D. |
(2014年山东临沂3分)在平面直角坐标系中,函数y=x2﹣2x(x≥0)的图象为C1,C1关于原点对称的图象为C2,则直线y=a(a为常数)与C1、C2的交点共有( )
| A.1个 | B.1个或2个 |
| C.个或2个或3个 | D.1个或2个或3个或4个 |
(2014年山东青岛3分)函数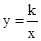 与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
A.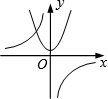 |
B. |
C.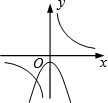 |
D.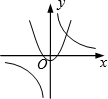 |
(2014年宁夏区3分)已知 ≠0,在同一直角坐标系中,函数
≠0,在同一直角坐标系中,函数 与
与 的图象有可能是( )
的图象有可能是( )
A. |
B. |
C. |
D. |
(2012广西贵港2分)若直线y=m(m为常数)与函数y=的图像恒有三个不同的交点,则常数m的取值范围是 。
(年福建龙岩10分)如图①,双曲线 (k≠0)和抛物线y=ax2+bx(a≠0)交于A、B、C三点,其中B(3,1),C(﹣1,﹣3),直线CO交双曲线于另一点D,抛物线与x轴交于另一点E.
(k≠0)和抛物线y=ax2+bx(a≠0)交于A、B、C三点,其中B(3,1),C(﹣1,﹣3),直线CO交双曲线于另一点D,抛物线与x轴交于另一点E.
(1)求双曲线和抛物线的解析式;
(2)抛物线在第一象限部分是否存在点P,使得∠POE+∠BCD=90°?若存在,请求出满足条件的点P的坐标;若不存在,请说明理由;
(3)如图②,过B作直线l⊥OB,过点D作DF⊥l于点F,BD与OF交于点N,求 的值.
的值.
(2014年福建漳州14分)已知抛物线l:y=ax2+bx+c(a,b,c均不为0)的顶点为M,与y轴的交点为N,我们称以N为顶点,对称轴是y轴且过点M的抛物线为抛物线l的衍生抛物线,直线MN为抛物线l的衍生直线.
(1)如图,抛物线y=x2﹣2x﹣3的衍生抛物线的解析式是 ,衍生直线的解析式是 ;
(2)若一条抛物线的衍生抛物线和衍生直线分别是y=﹣2x2+1和y=﹣2x+1,求这条抛物线的解析式;
(3)如图,设(1)中的抛物线y=x2﹣2x﹣3的顶点为M,与y轴交点为N,将它的衍生直线MN先绕点N旋转到与x轴平行,再沿y轴向上平移1个单位得直线n,P是直线n上的动点,是否存在点P,使△POM为直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.

(年广西崇左12分)在平面直角坐标系中,一次函数y=kx+b的图象与x轴、y轴分别相交于A(﹣3,0),B(0,﹣3)两点,二次函数y=x2+mx+n的图象经过点A.
(1)求一次函数y=kx+b的解析式;
(2)若二次函数y=x2+mx+n图象的顶点在直线AB上,求m,n的值;
(3)当﹣3≤x≤0时,二次函数y=x2+mx+n的最小值为﹣4,求m,n的值.
(年广西南宁10分)在平面直角坐标系中, 抛物线 与直线
与直线 交于A, B两点,点A在点B的左侧.
交于A, B两点,点A在点B的左侧.
(1)如图1,当 时,直接写出A,B两点的坐标;
时,直接写出A,B两点的坐标;
(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
(3)如图2,抛物线 与x轴交于C,D两点(点C在点D的左侧).在直线
与x轴交于C,D两点(点C在点D的左侧).在直线 上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时k的值;若不存在,请说明理由.
上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时k的值;若不存在,请说明理由.
(年广西玉林、防城港12分)给定直线l:y=kx,抛物线C:y=ax2+bx+1.
(1)当b=1时,l与C相交于A,B两点,其中A为C的顶点,B与A关于原点对称,求a的值;
(2)若把直线l向上平移k2+1个单位长度得到直线r,则无论非零实数k取何值,直线r与抛物线C都只有一个交点.
①求此抛物线的解析式;
②若P是此抛物线上任一点,过P作PQ∥y轴且与直线y=2交于Q点,O为原点.求证:OP=PQ.
(年贵州铜仁14分)已知:直线y=ax+b与抛物线 的一个交点为A(0,2),同时这条直线与x轴相交于点B,且相交所成的角β为45°.
的一个交点为A(0,2),同时这条直线与x轴相交于点B,且相交所成的角β为45°.
(1)求点B的坐标;
(2)求抛物线 的解析式;
的解析式;
(3)判断抛物线 与x轴是否有交点,并说明理由.若有交点设为M,N(点M在点N左边),将此抛物线关于y轴作轴反射得到M的对应点为E,轴反射后的像与原像相交于点F,连接NF,EF得△DEF,在原像上是否存在点P,使得△NEP的面积与△NEF的面积相等?若存在,请求出点P的坐标;若不存在,请说明理由.
与x轴是否有交点,并说明理由.若有交点设为M,N(点M在点N左边),将此抛物线关于y轴作轴反射得到M的对应点为E,轴反射后的像与原像相交于点F,连接NF,EF得△DEF,在原像上是否存在点P,使得△NEP的面积与△NEF的面积相等?若存在,请求出点P的坐标;若不存在,请说明理由.
(2014年黑龙江哈尔滨3分)如图,在△ABC中,4AB=5AC,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H.若点H是AC的中点,则 的值为 .
的值为 .

(年黑龙江牡丹江农垦10分)某体育用品商店试销一款成本为50元的排球,规定试销期间单价不低于成本价,且获利不得高于40%.经试销发现,销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系.
(1)试确定y与x之间的函数关系式;
(2)若该体育用品商店试销的这款排球所获得的利润Q元,试写出利润Q(元)与销售单价x(元)之间的函数关系式;当试销单价定为多少元时,该商店可获最大利润?最大利润是多少元?
(3)若该商店试销这款排球所获得的利润不低于600元,请确定销售单价x的取值范围.
(年湖北鄂州10分)大学生小张利用暑假50天在一超市勤工俭学,被安排销售一款成本为40元/件的新型商品,此类新型商品在第x天的销售量p件与销售的天数x的关系如下表:
| x(天) |
1 |
2 |
3 |
… |
50 |
| p(件) |
118 |
116 |
114 |
… |
20 |
销售单价q(元/件)与x满足:当1≤x<25时q=x+60;当25≤x≤50时 .
.
(1)请分析表格中销售量p与x的关系,求出销售量p与x的函数关系.
(2)求该超市销售该新商品第x天获得的利润y元关于x的函数关系式.
(3)这50天中,该超市第几天获得利润最大?最大利润为多少?
(年湖北武汉12分)如图,已知直线AB: 与抛物线
与抛物线 交于A、B两点,
交于A、B两点,
(1)直线AB总经过一个定点C,请直接写出点C坐标;
(2)当 时,在直线AB下方的抛物线上求点P,使△ABP的面积等于5;
时,在直线AB下方的抛物线上求点P,使△ABP的面积等于5;
(3)若在抛物线上存在定点D使∠ADB=90°,求点D到直线AB的最大距离.
(2014年湖北天门学业10分)某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作.已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果每千克的利润为3元,那么每天可售出250千克.
小红:如果以13元/千克的价格销售,那么每天可获取利润750元.
【利润=(销售价-进价) 销售量】
销售量】
(1)请根据他们的对话填写下表:
| 销售单价x(元/kg) |
10 |
11 |
13 |
| 销售量y(kg) |
|
|
|
(2)请你根据表格中的信息判断每天的销售量y(千克)与销售单价x(元)之间存在怎样的函数关系.并求y(千克)与x(元)(x>0)的函数关系式;
(3)设该超市销售这种水果每天获取的利润为W元,求W与x的函数关系式.当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?
(年湖南湘西22分)如图,抛物线y=ax2+bx+c关于y轴对称,它的顶点在坐标原点O,点B(2, )和点C(﹣3,﹣3)两点均在抛物线上,点F(0,
)和点C(﹣3,﹣3)两点均在抛物线上,点F(0, )在y轴上,过点(0,
)在y轴上,过点(0, )作直线l与x轴平行.
)作直线l与x轴平行.
(1)求抛物线的解析式和直线BC的解析式.
(2)设点D(x,y)是线段BC上的一个动点(点D不与B,C重合),过点D作x轴的垂线,与抛物线交于点G.设线段GD的长度为h,求h与x之间的函数关系式,并求出当x为何值时,线段GD的长度h最大,最大长度h的值是多少?
(3)若点P(m,n)是抛物线上位于第三象限的一个动点,连接PF并延长,交抛物线于另一点Q,过点Q作QS⊥l,垂足为点S,过点P作PN⊥l,垂足为点N,试判断△FNS的形状,并说明理由;
(4)若点A(﹣2,t)在线段BC上,点M为抛物线上的一个动点,连接AF,当点M在何位置时,MF+MA的值最小,请直接写出此时点M的坐标与MF+MA的最小值.
(年湖南益阳10分)如图,直线y=﹣3x+3与x轴、y轴分别交于点A、B,抛物线 经过点A、B,并与x轴交于另一点C,其顶点为P.
经过点A、B,并与x轴交于另一点C,其顶点为P.
(1)求a,k的值;
(2)抛物线的对称轴上有一点Q,使△ABQ是以AB为底边的等腰三角形,求Q点的坐标;
(3)在抛物线及其对称轴上分别取点M、N,使以A,C,M,N为顶点的四边形为正方形,求此正方形的边长.
(年湖南张家界12分)如图,在平面直角坐标系中,O为坐标原点,抛物线过 过O、B、C三点,B、C坐标分别为(10,0)和(
过O、B、C三点,B、C坐标分别为(10,0)和( ,
, ),以OB为直径的⊙A经过C点,直线l垂直于x轴于点B.
),以OB为直径的⊙A经过C点,直线l垂直于x轴于点B.
(1)求直线BC的解析;
(2)求抛物线解析式及顶点坐标;
(3)点M是⊙A上一动点(不同于O,B),过点M作⊙A的切线,交y轴于点E,交直线l于点F,设线段ME长为m ,MF长为n,请猜想 的值,并证明你的结论;
的值,并证明你的结论;
(4)点P从O出发,以每秒1个单位速度向点B作直线运动,点Q同时从B出发,以相同速度向点C作直线运动,经过t(0<t )秒时恰好使△BPQ为等腰三角形,请求出满足条件的t值.
)秒时恰好使△BPQ为等腰三角形,请求出满足条件的t值.
(年湖南长沙10分)在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为“梦之点”,例如点(﹣1,﹣1),(0,0),( ,
, ),…都是“梦之点”,显然,这样的“梦之点”有无数个.
),…都是“梦之点”,显然,这样的“梦之点”有无数个.
(1)若点P(2,m)是反比例函数 (n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;
(n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;
(2)函数y=3kx+s﹣1(k,s是常数)的图象上存在“梦之点”吗?若存在,请求出“梦之点”的坐标;若不存在,请说明理由;
(3)若二次函数y=ax2+bx+1(a,b是常数,a>0)的图象上存在两个不同的“梦之点”A(x1,x1),B(x2,x2),且满足﹣2<x1<2,|x1﹣x2|=2,令t=b2﹣2b+ ,试求出t的取值范围.
,试求出t的取值范围.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号