（年贵州铜仁14分）已知：直线y=ax+b与抛物线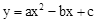
的一个交点为A（0，2），同时这条直线与x轴相交于点B，且相交所成的角β为45°．
（1）求点B的坐标；
（2）求抛物线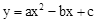的解析式；
（3）判断抛物线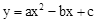与x轴是否有交点，并说明理由．若有交点设为M，N（点M在点N左边），将此抛物线关于y轴作轴反射得到M的对应点为E，轴反射后的像与原像相交于点F，连接NF，EF得△DEF，在原像上是否存在点P，使得△NEP的面积与△NEF的面积相等？若存在，请求出点P的坐标；若不存在，请说明理由．
（年贵州铜仁14分）已知：直线y=ax+b与抛物线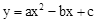的一个交点为A（0，2），同时这条直线与x轴相交于点B，且相交所成的角β为45°．
（1）求点B的坐标；
（2）求抛物线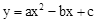的解析式；
（3）判断抛物线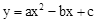与x轴是否有交点，并说明理由．若有交点设为M，N（点M在点N左边），将此抛物线关于y轴作轴反射得到M的对应点为E，轴反射后的像与原像相交于点F，连接NF，EF得△DEF，在原像上是否存在点P，使得△NEP的面积与△NEF的面积相等？若存在，请求出点P的坐标；若不存在，请说明理由．
km，冥王星和太阳的平均距离约是水星和太阳的平均距离的102倍，那么冥王星和太阳的平均距离约为多少km？
次运算，它工作5×10
秒可作多少次运算？
·a
-2a
·a
-3a
·a
.
·（2x-y）·（2x-y）
；
）
·（
；
粤公网安备 44130202000953号