（年福建龙岩10分）如图①，双曲线
（k≠0）和抛物线y=ax2+bx（a≠0）交于A、B、C三点，其中B（3，1），C（﹣1，﹣3），直线CO交双曲线于另一点D，抛物线与x轴交于另一点E．
（1）求双曲线和抛物线的解析式；
（2）抛物线在第一象限部分是否存在点P，使得∠POE+∠BCD=90°？若存在，请求出满足条件的点P的坐标；若不存在，请说明理由；
（3）如图②，过B作直线l⊥OB，过点D作DF⊥l于点F，BD与OF交于点N，求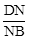
的值．
相关试题
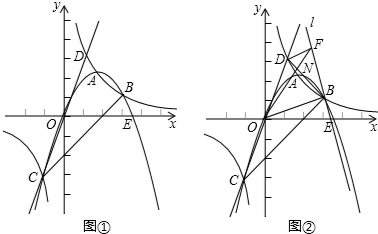
（年福建龙岩10分）如图①，双曲线（k≠0）和抛物线y=ax2+bx（a≠0）交于A、B、C三点，其中B（3，1），C（﹣1，﹣3），直线CO交双曲线于另一点D，抛物线与x轴交于另一点E．
（1）求双曲线和抛物线的解析式；
（2）抛物线在第一象限部分是否存在点P，使得∠POE+∠BCD=90°？若存在，请求出满足条件的点P的坐标；若不存在，请说明理由；
（3）如图②，过B作直线l⊥OB，过点D作DF⊥l于点F，BD与OF交于点N，求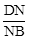的值．
粤公网安备 44130202000953号