(年湖南益阳10分)如图,直线y=﹣3x+3与x轴、y轴分别交于点A、B,抛物线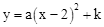 经过点A、B,并与x轴交于另一点C,其顶点为P.
经过点A、B,并与x轴交于另一点C,其顶点为P.
(1)求a,k的值;
(2)抛物线的对称轴上有一点Q,使△ABQ是以AB为底边的等腰三角形,求Q点的坐标;
(3)在抛物线及其对称轴上分别取点M、N,使以A,C,M,N为顶点的四边形为正方形,求此正方形的边长.
(年湖南益阳10分)如图,直线y=﹣3x+3与x轴、y轴分别交于点A、B,抛物线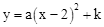 经过点A、B,并与x轴交于另一点C,其顶点为P.
经过点A、B,并与x轴交于另一点C,其顶点为P.
(1)求a,k的值;
(2)抛物线的对称轴上有一点Q,使△ABQ是以AB为底边的等腰三角形,求Q点的坐标;
(3)在抛物线及其对称轴上分别取点M、N,使以A,C,M,N为顶点的四边形为正方形,求此正方形的边长.