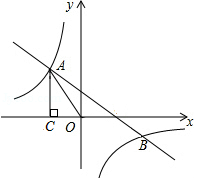
在 中, 边的长为 , 边上的高为 , 的面积为2.
(1) 关于 的函数关系式是 , 的取值范围是 ;
(2)在平面直角坐标系中画出该函数图象;
(3)将直线 向上平移 个单位长度后与上述函数图象有且只有一个交点,请求出此时 的值.
经过实验获得两个变量 , 的一组对应值如下表.
|
1 |
2 |
3 |
4 |
5 |
6 |
|
6 |
2.9 |
2 |
1.5 |
1.2 |
1 |
(1)请画出相应函数的图象,并求出函数表达式.
(2)点 , , , 在此函数图象上.若 ,则 , 有怎样的大小关系?请说明理由.
请用学过的方法研究一类新函数 为常数, 的图象和性质.
(1)在给出的平面直角坐标系中画出函数 的图象;
(2)对于函数 ,当自变量 的值增大时,函数值 怎样变化?
如图,直线 与 轴交于点 ,与 轴交于点 ,将线段 绕点 顺时针旋转 得到线段 ,反比例函数 的图象经过点 .
(1)求直线 和反比例函数 的解析式;
(2)已知点 是反比例函数 图象上的一个动点,求点 到直线 距离最短时的坐标.

已知反比例函数 y= 的图象在二四象限,一次函数为 y= kx+ b( b>0),直线 x=1与 x轴交于点 B,与直线 y= kx+ b交于点 A,直线 x=3与 x轴交于点 C,与直线 y= kx+ b交于点 D.
(1)若点 A, D都在第一象限,求证: b>﹣3 k;
(2)在(1)的条件下,设直线 y= kx+ b与 x轴交于点 E与 y轴交于点 F,当 = 且△ OFE的面积等于 时,求这个一次函数的解析式,并直接写出不等式 > kx+ b的解集.
九年级某数学兴趣小组在学习了反比例函数的图象与性质后,进一步研究了函数 的图象与性质共探究过程如下:
(1)绘制函数图象,如图1.
列表:下表是 与 的几组对应值,其中 ;
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
|
|
|
1 |
2 |
4 |
4 |
2 |
|
|
|
描点:根据表中各组对应值 ,在平面直角坐标系中描出了各点;
连线:用平滑的曲线顺次连接各点,画出了部分图象.请你把图象补充完整;
(2)通过观察图1,写出该函数的两条性质;
① ;
② ;
(3)①观察发现:如图2.若直线 交函数 的图象于 , 两点,连接 ,过点 作 交 轴于 .则 ;
②探究思考:将①中"直线 "改为"直线 ",其他条件不变,则 ;
③类比猜想:若直线 交函数 的图象于 , 两点,连接 ,过点 作 交 轴于 ,则 .

若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数.下面我们参照学习函数的过程与方法,探究分段函数的图象与性质.列表:
0 |
1 |
2 |
3 |
||||||||||||
1 |
2 |
1 |
0 |
1 |
2 |
描点:在平面直角坐标系中,以自变量的取值为横坐标,以相应的函数值
为纵坐标,描出相应的点,如图所示.
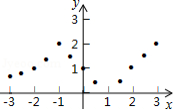
(1)如图,在平面直角坐标系中,观察描出的这些点的分布,作出函数图象;
(2)研究函数并结合图象与表格,回答下列问题:
①点,
,
,
,
,
,
在函数图象上,则
,
;(填“
”,“
”或“
”
②当函数值时,求自变量
的值;
③在直线的右侧的函数图象上有两个不同的点
,
,
,
,且
,求
的值;
④若直线与函数图象有三个不同的交点,求
的取值范围.
(1)阅读理解
如图,点,
在反比例函数
的图象上,连接
,取线段
的中点
.分别过点
,
,
作
轴的垂线,垂足为
,
,
,
交反比例函数
的图象于点
.点
,
,
的横坐标分别为
,
,
.
小红通过观察反比例函数的图象,并运用几何知识得出结论:
,
由此得出一个关于,
,
,之间数量关系的命题:
若,则
.
(2)证明命题
小东认为:可以通过“若,则
”的思路证明上述命题.
小晴认为:可以通过“若,
,且
,则
”的思路证明上述命题.
请你选择一种方法证明(1)中的命题.

如图,一次函数的图象与反比例函数
的图象交于第二、四象限内的点
和点
.过点
作
轴的垂线,垂足为点
,
的面积为4.
(1)分别求出和
的值;
(2)结合图象直接写出的解集;
(3)在轴上取点
,使
取得最大值时,求出点
的坐标.