(1)阅读理解
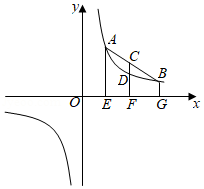
如图,点,在反比例函数的图象上,连接,取线段的中点.分别过点,,作轴的垂线,垂足为,,,交反比例函数的图象于点.点,,的横坐标分别为,,.
小红通过观察反比例函数的图象,并运用几何知识得出结论:
,
由此得出一个关于,,,之间数量关系的命题:
若,则 .
(2)证明命题
小东认为:可以通过“若,则”的思路证明上述命题.
小晴认为:可以通过“若,,且,则”的思路证明上述命题.
请你选择一种方法证明(1)中的命题.
相关知识点
推荐套卷
(1)阅读理解
如图,点,在反比例函数的图象上,连接,取线段的中点.分别过点,,作轴的垂线,垂足为,,,交反比例函数的图象于点.点,,的横坐标分别为,,.
小红通过观察反比例函数的图象,并运用几何知识得出结论:
,
由此得出一个关于,,,之间数量关系的命题:
若,则 .
(2)证明命题
小东认为:可以通过“若,则”的思路证明上述命题.
小晴认为:可以通过“若,,且,则”的思路证明上述命题.
请你选择一种方法证明(1)中的命题.
