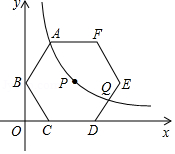
如图，在平面直角坐标系中，正六边形的对称中心在反比例函数的图象上，边在轴上，点在轴上，已知．
（1）点是否在该反比例函数的图象上？请说明理由；
（2）若该反比例函数图象与交于点，求点的横坐标；
（3）平移正六边形，使其一边的两个端点恰好都落在该反比例函数的图象上，试描述平移过程．
分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE．已知∠ACB＝90°、∠BAC＝30°，EF⊥AB，垂足为F，连接DF、CF．
（1）试说明AC＝EF；
（2）求证：四边形ADFE是平行四边形；
（3）找出图中除△ACD、△ABE以外的等边三角形，并说明理由．
的一元二次方程
－4
＝0有两个不相等的实数根，请你选择一个
－4|－22＋
－3×（－4）．如图，在平面直角坐标系中，点A的坐标为（7，0），点B的坐标为（3，4），
（1）求经过O、A、B三点的抛物线解析式；
（2）将线段AB绕A点顺时针旋转75°至AC，直接写出点C的坐标.
（3）在y轴上找一点P，第一象限找一点Q，使得以O、B、Q、P为顶点的四边形是菱形，求出点Q的坐标；
（4）△OAB的边OB上有一动点M，过M作MN//OA交AB于N，将△BMN沿MN翻折得△DMN，设MN=x，△DMN与△OAB重叠部分的面积为y，求出y与x之间的函数关系式，并求出重叠部分面积的最大值.
黄冈市某高新企业制定工龄工资标准时充分考虑员工对企业发展的贡献，同时提高员工的积极性、控制员工的流动率，对具有中职以上学历员工制定如下的工龄工资方案。
Ⅰ.工龄工资分为社会工龄工资和企业工龄工资；
Ⅱ.社会工龄=参加本企业工作时年龄－18，
企业工龄=现年年龄－参加本企业工作时年龄。
Ⅲ.当年工作时间计入当年工龄
Ⅳ.社会工龄工资y1（元/月）与社会工龄x（年）之间的函数关系式如①图所示，企业工龄工资y2（元/月）与企业工龄x（年）之间的函数关系如图②所示.
请解决以下问题
（1）求出y1、y2与工龄x之间的函数关系式；
（2）现年28岁的高级技工小张从18岁起一直在深圳实行同样工龄工资制度的外地某企业工作，为了方便照顾老人与小孩，今年小张回乡应聘到该企业，试计算第一年工龄工资每月下降多少元？
（3）已经在该企业工作超过3年的李工程师今年48岁，试求出他的工资最高每月多少元？
粤公网安备 44130202000953号