初中数学一元二次方程解答题

某网络经销商销售一款夏季时装，进价每件60元，售价每件130元，每天销售30件，每销售一件需缴纳网络平台管理费4元．未来30天，这款时装将开展“每天降价1元”的促销活动，即从第一天起每天的单价均比前一天降1元，通过市场调查发现，该时装单价每降1元，每天销售量增加5件，设第 $x$天 $(1⩽x⩽30$且 $x$为整数）的销量为 $y$件．

（1）直接写出 $y$与 $x$的函数关系式；

（2）在这30天内，哪一天的利润是6300元？

（3）设第 $x$天的利润为 $W$元，试求出 $W$与 $x$之间的函数关系式，并求出哪一天的利润最大，最大利润是多少．

小李在景区销售一种旅游纪念品，已知每件进价为6元，当销售单价定为8元时，每天可以销售200件．市场调查反映：销售单价每提高1元，日销量将会减少10件，物价部门规定：销售单价不能超过12元，设该纪念品的销售单价为 $x$（元 $)$，日销量为 $y$（件 $)$，日销售利润为 $w$（元 $)$．

（1）求 $y$与 $x$的函数关系式．

（2）要使日销售利润为720元，销售单价应定为多少元？

（3）求日销售利润 $w$（元 $)$与销售单价 $x$（元 $)$的函数关系式，当 $x$为何值时，日销售利润最大，并求出最大利润．

某村2016年的人均收入为20000元，2018年的人均收入为24200元

（1）求2016年到2018年该村人均收入的年平均增长率；

（2）假设2019年该村人均收入的增长率与前两年的年平均增长率相同，请你预测2019年该村的人均收入是多少元？

某公司今年1月份的生产成本是400万元，由于改进技术，生产成本逐月下降，3月份的生产成本是361万元．

假设该公司2、3、4月每个月生产成本的下降率都相同．

（1）求每个月生产成本的下降率；

（2）请你预测4月份该公司的生产成本．

若三个非零实数 $x$， $y$， $z$满足：只要其中一个数的倒数等于另外两个数的倒数的和，则称这三个实数 $x$， $y$， $z$构成“和谐三组数”．

（1）实数1，2，3可以构成“和谐三组数”吗？请说明理由；

（2）若 $M(t,y_1)$， $N(t+1,y_2)$， $R(t+3,y_3)$三点均在函数 $y=\frac{k}{x}(k$为常数， $k\ne 0)$的图象上，且这三点的纵坐标 $y_1$， $y_2$， $y_3$构成“和谐三组数”，求实数 $t$的值；

（3）若直线 $y=2\mathit{bx}+2c(\mathit{bc}\ne 0)$与 $x$轴交于点 $A(x_1$， $0)$，与抛物线 $y=a{x}^2+3\mathit{bx}+3c(a\ne 0)$交于 $B(x_2$， $y_2)$， $C(x_3$， $y_3)$两点．

①求证： $A$， $B$， $C$三点的横坐标 $x_1$， $x_2$， $x_3$构成“和谐三组数”；

②若 $a>2b>3c$， $x_2=1$，求点 $P(\frac{c}{a}$， $\frac{b}{a})$与原点 $O$的距离 $\mathit{OP}$的取值范围．

由多项式乘法： $(x+a)(x+b)=x^2+(a+b)x+\mathit{ab}$，将该式从右到左使用，即可得到“十字相乘法”进行因式分解的公式： $x^2+(a+b)x+\mathit{ab}=(x+a)(x+b)$．

示例：分解因式： $x^2+5x+6=x^2+(2+3)x+2\times 3=(x+2)(x+3)$．

（1）尝试：分解因式： $x^2+6x+8=(x+$　　 $\left)\right(x+$　　 $)$；

（2）应用：请用上述方法解方程： $x^2-3x-4=0$．

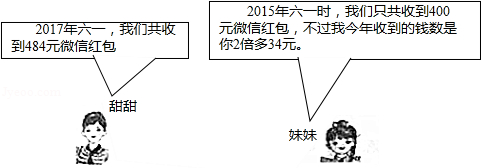
收发微信红包已成为各类人群进行交流联系、增强感情的一部分，下面是甜甜和她的双胞胎妹妹在六一儿童节期间的对话．

请问：（1）2015年到2017年甜甜和她妹妹在六一收到红包的年增长率是多少？

（2）2017年六一甜甜和她妹妹各收到了多少钱的微信红包？

在水果销售旺季，某水果店购进一优质水果，进价为20元 $/$千克，售价不低于20元 $/$千克，且不超过32元 $/$千克，根据销售情况，发现该水果一天的销售量 $y$（千克）与该天的售价 $x$（元 $/$千克）满足如下表所示的一次函数关系．

销售量 $y$（千克）	$\dots$	34.8	32	29.6	28	$\dots$
售价 $x$（元 $/$千克）	$\dots$	22.6	24	25.2	26	$\dots$

（1）某天这种水果的售价为23.5元 $/$千克，求当天该水果的销售量．

（2）如果某天销售这种水果获利150元，那么该天水果的售价为多少元？

某地2015年为做好“精准扶贫”，投入资金1280万元用于异地安置，并规划投入资金逐年增加，2017年在2015年的基础上增加投入资金1600万元．

（1）从2015年到2017年，该地投入异地安置资金的年平均增长率为多少？

（2）在2017年异地安置的具体实施中，该地计划投入资金不低于500万元用于优先搬迁租房奖励，规定前1000户（含第1000户）每户每天奖励8元，1000户以后每户每天奖励5元，按租房400天计算，求2017年该地至少有多少户享受到优先搬迁租房奖励．

某商店以20元 $/$千克的单价新进一批商品，经调查发现，在一段时间内，销售量 $y$（千克）与销售单价 $x$（元 $/$千克）之间为一次函数关系，如图所示．

（1）求 $y$与 $x$的函数表达式；

（2）要使销售利润达到800元，销售单价应定为每千克多少元？

已知关于 $x$的一元二次方程： $x^2-(t-1)x+t-2=0$．

（1）求证：对于任意实数 $t$，方程都有实数根；

（2）当 $t$为何值时，方程的两个根互为相反数？请说明理由．

为进一步发展基础教育，自2014年以来，某县加大了教育经费的投入，2014年该县投入教育经费6000万元．2016年投入教育经费8640万元．假设该县这两年投入教育经费的年平均增长率相同．

（1）求这两年该县投入教育经费的年平均增长率；

（2）若该县教育经费的投入还将保持相同的年平均增长率，请你预算2017年该县投入教育经费多少万元．

已知关于 $x$的一元二次方程： $x^2-2x-k-2=0$有两个不相等的实数根．

（1）求 $k$的取值范围；

（2）给 $k$取一个负整数值，解这个方程．

某养殖场为了响应党中央的扶贫政策，今年起采用“场内 $+$农户”养殖模式，同时加强对蛋鸡的科学管理，蛋鸡的产蛋率不断提高，三月份和五月份的产蛋量分别是2.5万 $\mathit{kg}$与3.6万 $\mathit{kg}$，现假定该养殖场蛋鸡产蛋量的月增长率相同．

（1）求该养殖场蛋鸡产蛋量的月平均增长率；

（2）假定当月产的鸡蛋当月在各销售点全部销售出去，且每个销售点每月平均销售量最多为0.32万 $\mathit{kg}$．如果要完成六月份的鸡蛋销售任务，那么该养殖场在五月份已有的销售点的基础上至少再增加多少个销售点？

2016年，某贫困户的家庭年人均纯收入为2500元，通过政府产业扶持，发展了养殖业后，到2018年，家庭年人均纯收入达到了3600元．

（1）求该贫困户2016年到2018年家庭年人均纯收入的年平均增长率；

（2）若年平均增长率保持不变，2019年该贫困户的家庭年人均纯收入是否能达到4200元？