初中数学整式的加减解答题

本题8分）便民超市原有桶食用油，上午卖出桶食用油，中午休息时又购进同样的食用油桶，下班清仓时发现该食用油只剩下5桶，请问：
（1）便民超市中午过后一共卖出多少桶食用油（用含的式子表示）？
（2）当时，便民超市这一天共卖出多少桶食用油？

轮船在静水中的速度为  km/h，水流速度为 km/h，轮船顺水航行4 h,逆水航行3 h，轮船一共行驶了多少km？（结果用含，的式子表示）

（1）先化简再求值：求的值，其中 .
（2）已知A，B，且多项式的值与字母的取值无关，求的值.

将连续的奇数1，3，5，7…排列成如下的数表用十字框框出5个数（如图），

（1）若将十字框上下左右平移，但一定要框住数列中的5个数，若设中间的数为a，用a的代数式表示十字框框住的5个数字之和；
（2）十字框框住的5个数之和能等于2020吗？若能，分别写出十字框框住的5个数；若不能，请说明理由；
（3）十字框框住的5个数之和能等于365吗？若能，分别写出十字框框住的5个数；若不能，请说明理由．（本题6分）

（1）写出一个含有字母x的代数式，当x =1时，代数式的值等于2；
（2）写出一个含有字母x的代数式，当x =4和x =时，代数式的值都等于5；
（3）写出两个只含有字母x的二次三项式，当x不论取什么值时，这两个多项式的和总是等于3（列式表示）．

先化简，再求值，其中．

如图①所示是一个长为2m，宽为2n的长方形，沿图中虚线用剪刀均分成四个小长方形，然后按图②的方式拼成一个正方形．

（1）你认为图②中的阴影部分的正方形的边长等于        ．
（2）请用两种不同的方法列代数式表示图②中阴影部分的面积，
方法①                    ．方法②                    ．
（3）观察图②，你能写出（m＋n）²，（m－n）²，mn这三个代数式之间的等量关系吗？
（4）根据（3）题中的等量关系，解决如下问题：若a＋b＝6，ab＝4，则求（a－b）²的值．

在数的学习过程中，我们总会对其中一些具有某种特性的数进行研究，如学习自然数时，我们研究了偶数、奇数、合数、质数等．现在我们来研究一种特殊的自然数 “纯数”．

定义：对于自然数，在通过列竖式进行的运算时各位都不产生进位现象，则称这个自然数为“纯数”．

例如：32是“纯数”，因为在列竖式计算时各位都不产生进位现象；23不是“纯数”，因为在列竖式计算时个位产生了进位．

（1）请直接写出1949到2019之间的“纯数”；

（2）求出不大于100的“纯数”的个数，并说明理由．

有一电脑程序：每按一次按键，屏幕的 $A$ 区就会自动加上 $a^2$ ，同时 $B$ 区就会自动减去 $3a$ ，且均显示化简后的结果．已知 $A$ ， $B$ 两区初始显示的分别是25和 $-16$ ，如图．

如，第一次按键后， $A$ ， $B$ 两区分别显示：

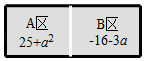
（1）从初始状态按2次后，分别求 $A$ ， $B$ 两区显示的结果；

（2）从初始状态按4次后，计算 $A$ ， $B$ 两区代数式的和，请判断这个和能为负数吗？说明理由．

先化简，再求值： $5(3a^{2}b-a{b}^2)-3(a{b}^2+5a^{2}b)$ ，其中 $a=\frac{1}{3}$ ， $b=-\frac{1}{2}$ ．

课堂上李老师把要化简求值的整式（7a²﹣6a²b+3a²b）﹣（﹣3a²﹣6a²b+3a²b+10a²﹣3）写完后，让王红同学任意给出一组a、b的值，老师自己说答案，当王红说完：“a=38，b=﹣32”后，李老师不假思索，立刻就说出答案“3”．同学们莫名其妙，觉得不可思议，但李老师用坚定的口吻说：“这个答案准确无误”，亲爱的同学你相信吗？请你通过计算说出其中的道理．

化简：
（1）2（2x-3y）-（3x+2y+1）；
（2）-（3a²-4ab）+[a²-2（2a+2ab）]．

有理数x、y在数轴上对应点如图所示：

（1）在数轴上表示、；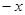
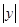（2）试把x、y、0、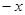、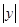这五个数从小到大用“＜”号连接；
（3）化简．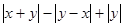

化简：
（1）；
（2）．

先化简，再求值：（x﹣2）（x+2）+x²（x﹣1），其中x=﹣1．