江苏省无锡市南长区七年级上学期期中考试数学试卷
下列各数- ,0,(-
,0,(- )2,
)2, ,π,|-3.4|中,正分数有( )
,π,|-3.4|中,正分数有( )
| A.3个 | B.4个 | C.5个 | D.6个 |
下列各组数中,数值相等的是( )
| A.34和43 |
| B.-42和(-4)2 |
| C.-23和(-2)3 |
| D.(-2×3)2和-22×32 |
若(m-2)x|m|-1=5是关于x的一元一次方程,则m的值为( )
| A.±2 | B.-2 | C.2 | D.4 |
如果a+b>0,ab<0,那么( )
| A.a>0,b>0 | B.a、b异号且负数的绝对值较大 |
| C.a<0,b<0 | D.a、b异号且负数的绝对值较小 |
下列说法中正确的个数有( )
①0是绝对值最小的有理数;
②无限小数是无理数;
③数轴上原点两侧的数互为相反数;
④a,0, 都是单项式;
都是单项式;
⑤单项式- 的系数为-2,次数是3;
的系数为-2,次数是3;
⑥ 是关于x,y的三次三项式,常数项是-1.
是关于x,y的三次三项式,常数项是-1.
| A.2个 | B.3个 | C.4个 | D.5个 |
数a、b在数轴上如图所示,化简|b+a|-2|b-a|的值为 ( )

| A.3a-b | B.3b-a | C.a-3b | D.b-3a |
如图,点A、B对应的数是a、b,点A在-3,-2对应的两点(包括这两点)之间移动,点B在-1,0对应的两点(包括这两点)之间移动,则以下四个代数式的值,可能比2013大的是 ………( )

A.b-a B. C.(a-b)2 D.
C.(a-b)2 D. -
-
我国第六次全国人口普查中,具有大学(指大专以上)文化程度的人口约为120 000 000人,将这个数据用科学记数法可表示为 人.
如果x=3时,式子px3+qx+1的值为2011,则当x=-3时,式子px3+qx+1的值是 .
定义:f (a,b)=(b,a ),g(m,n)=(-m,-n ).例如f (2,3)=(3,2 ),g(-1,-4)=(1,4),则g(f(-5,6)) =____________.
若“!”是一种数学运算符号,并且1!=1,2!=2×1,3!=3×2×1,4!=4×3×2×1,…则 的值为 .
的值为 .
国数学家洛萨提出了一个猜想:如果n为奇数 ,我们计算3n+1;如果n为偶数,我们除以2,不断重复这样的运算,经过有限步骤后一定可以得到1.例如,n=5时,经过上述运算,依次得到一列数5,16,8,4,2,1.( 注:计算到1结束),若n=12,得到一列数的和为 ;若小明同学对某个整数n,按照上述运算,得到一列数,已知第八个数为1,则整数n的所有可能取值中,最小的值为 .
计算
(1)-3-(-14)-10+(-2)
(2)102+(-2)2×(-5)
(3)( -1
-1 +
+ )÷(-
)÷(- )
)
(4)-14- ×[2-(-3)2]
×[2-(-3)2]
解答
(1)化简及求值5(3a2b-2ab2)-4(-2 ab2+3a2b) ,其中a、b满足|a+2|+(b-1)2=0. (2)已知x+y=
(2)已知x+y= ,xy=-
,xy=- .求代数式(x+3y-3xy) -2(xy-2 x-y) 的值.
.求代数式(x+3y-3xy) -2(xy-2 x-y) 的值.
为庆祝我国首个空间实验室“天宫一号”顺利升空,学校开展了火箭模型制作比赛,如图为火箭模型的截面图,下面是梯形,中间是长方形,上面是三角形.
(1)用a、b的代数式表示该截面的面积S;
(2)当a=2cm,b=3cm时,求这个截面的面积.
如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.

(1)你认为图②中的阴影部分的正方形的边长等于 .
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积,
方法① .方法② .
(3)观察图②,你能写出(m+n)2,(m-n)2,mn这三个代数式之间的等量关系吗?
(4)根据(3)题中的等量关系,解决如下问题:若a+b=6,ab=4,则求(a-b)2的值.

 的绝对值是 ,-
的绝对值是 ,- 的倒数是 .
的倒数是 .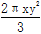 的系数是 ,次数是 .
的系数是 ,次数是 .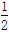 x2yn的差仍为单项式,则它们的差为 .
x2yn的差仍为单项式,则它们的差为 . 的大小关系是 .
的大小关系是 . 的值是整数,则整数
的值是整数,则整数 的值为 .
的值为 . =
= +1
+1
 粤公网安备 44130202000953号
粤公网安备 44130202000953号