为庆祝我国首个空间实验室“天宫一号”顺利升空，学校开展了火箭模型制作比赛，如图为火箭模型的截面图，下面是梯形，中间是长方形，上面是三角形．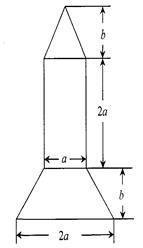
（1）用a、b的代数式表示该截面的面积S；
（2）当a＝2cm，b＝3cm时，求这个截面的面积．
相关试题
．
，再选择一个恰当的x值代入并求值．
．
与
轴交于点
，与
轴交于点A、B，点A的坐标为（4，0）
推荐套卷
为庆祝我国首个空间实验室“天宫一号”顺利升空，学校开展了火箭模型制作比赛，如图为火箭模型的截面图，下面是梯形，中间是长方形，上面是三角形．
（1）用a、b的代数式表示该截面的面积S；
（2）当a＝2cm，b＝3cm时，求这个截面的面积．
粤公网安备 44130202000953号