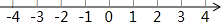初中数学有理数的混合运算解答题

观察下列等式：

$2+2^2=2^3-2$ ；

$2+2^2+2^3=2^4-2$ ；

$2+2^2+2^3+2^4=2^5-2$ ；

$2+2^2+2^3+2^4+2^5=2^6-2$ ；

$\dots$

已知按一定规律排列的一组数： $2^{20}$ ， $2^{21}$ ， $2^{22}$ ， $2^{23}$ ， $2^{24}$ ， $\dots$ ， $2^{38}$ ， $2^{39}$ ， $2^{40}$ ，若 $2^{20}=m$ ，则 $2^{20}+2^{21}+2^{22}+2^{23}+2^{24}+\dots +2^{38}+2^{39}+2^{40}=$ 　 　（结果用含 $m$ 的代数式表示）．

阅读下列材料：小明为了计算的值，采用以下方法：

设①

则②

②①得

请仿照小明的方法解决以下问题：

（1）　　；

（2）　　；

（3）求的和，是正整数，请写出计算过程）．

求两个正整数的最大公约数是常见的数学问题，中国古代数学专著《九章算术》中便记载了求两个正整数最大公约数的一种方法 $--$更相减损术，术曰：“可半者半之，不可半者，副置分母、子之数，以少成多，更相减损，求其等也．以等数约之”，意思是说，要求两个正整数的最大公约数，先用较大的数减去较小的数，得到差，然后用减数与差中的较大数减去较小数，以此类推，当减数与差相等时，此时的差（或减数）即为这两个正整数的最大公约数．

例如：求91与56的最大公约数

解：

请用以上方法解决下列问题：

（1）求108与45的最大公约数；

（2）求三个数78、104、143的最大公约数．

在" $-$ "" $\times$ "两个符号中选一个自己想要的符号，填入 $2^2+2\times (1$ □ $\frac{1}{2})$ 中的□，并计算．

我们知道，任意一个正整数 $n$ 都可以进行这样的分解： $n=p\times q(p$ ， $q$ 是正整数，且 $p⩽q)$ ，在 $n$ 的所有这种分解中，如果 $p$ ， $q$ 两因数之差的绝对值最小，我们就称 $p\times q$ 是 $n$ 的最佳分解．并规定： $F\left(n\right)=\frac{p}{q}$ ．例如12可以分解成 $1\times 12$ ， $2\times 6$ 或 $3\times 4$ ，因为 $12-1>6-2>4-3$ ，所以 $3\times 4$ 是12的最佳分解，所以 $F\left(12\right)=\frac{3}{4}$ ．

（1）如果一个正整数 $a$ 是另外一个正整数 $b$ 的平方，我们称正整数 $a$ 是完全平方数．求证：对任意一个完全平方数 $m$ ，总有 $F\left(m\right)=1$ ；

（2）如果一个两位正整数 $t$ ， $t=10x+y(1⩽x⩽y⩽9$ ， $x$ ， $y$ 为自然数），交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18，那么我们称这个数 $t$ 为"吉祥数"，求所有"吉祥数"中 $F\left(t\right)$ 的最大值．

（1）计算： ${(-4)}^2\times {(-\frac{1}{2})}^3-(-4+1)$．

（2）下面是小彬同学进行分式化简的过程，请认真阅读并完成相应任务．

$\frac{x^2-9}{x^2+6x+9}-\frac{2x+1}{2x+6}$

$=\frac{(x+3)(x-3)}{{(x+3)}^2}-\frac{2x+1}{2(x+3)}\dots$第一步

$=\frac{x-3}{x+3}-\frac{2x+1}{2(x+3)}\dots$第二步

$=\frac{2(x-3)}{2(x+3)}-\frac{2x+1}{2(x+3)}\dots$第三步

$=\frac{2x-6-(2x+1)}{2(x+3)}\dots$第四步

$=\frac{2x-6-2x+1}{2(x+3)}\dots$第五步

$=-\frac{5}{2x+6}\dots$第六步

任务一：填空：

①以上化简步骤中，第　　步是进行分式的通分，通分的依据是　　．或填为：　　；

②第　　步开始出现错误，这一步错误的原因是　　；

任务二：请直接写出该分式化简后的正确结果；

任务三：除纠正上述错误外，请你根据平时的学习经验，就分式化简时还需要注意的事项给其他同学提一条建议．

计算：．

（1）计算： ${(-1)}^4\times |-8|+{(-2)}^3\times {\left(\frac{1}{2}\right)}^2$ ．

（2）下面是小明同学解不等式的过程，请认真阅读并完成相应任务．

$\frac{2x-1}{3}>\frac{3x-2}{2}-1$ ．

解： $2(2x-1)>3(3x-2)-6\dots \dots$ 第一步

$4x-2>9x-6-6\dots \dots$ 第二步

$4x-9x>-6-6+2\dots \dots$ 第三步

$-5x>-10\dots \dots$ 第四步

$x>2\dots \dots$ 第五步

任务一：填空：①以上解题过程中，第二步是依据 　  　（运算律）进行变形的；

②第 　　步开始出现错误，这一步错误的原因是 　　；

任务二：请直接写出该不等式的正确解集．

计算：．

设a，b是任意两个实数，规定a与b之间的一种运算“⊕”为： $a\oplus b\left\{\begin{array}{c}\frac{b}{a}(a>0)\\ a-b(a\le 0)\end{array}\right.$，

例如： $1\oplus (-3)=\frac{-3}{1}=-3,(-3)\oplus 2=(-3)-2=-5$，

$\left(x^2+1\right)\oplus (x-1)=\frac{x-1}{x^2+1}$（因为 $x^2+1＞0$）

参照上面材料，解答下列问题：

（1） $2\oplus 4＝$　　， $\mathit{（﹣}2）\oplus 4=$　　；

（2）若 $x>\frac{1}{2}$，且满足 $（2x-1）\oplus （4x^2-1\mathit{）＝（﹣}4）\oplus （1-4x）$，求x的值．

阅读以下材料：

苏格兰数学家纳皮尔 $(J$． $\mathit{Npler}$， $1550-1617$年）是对数的创始人．他发明对数是在指数书写方式之前，直到18世纪瑞士数学家欧拉 $(\mathit{Evler}$， $1707-1783$年）才发现指数与对数之间的联系．

对数的定义：一般地，若 $a^x=N(a>0$且 $a\ne 1)$，那么 $x$叫做以 $a$为底 $N$的对数，记作 $x={\log }_{a}N$，比如指数式 $2^4=16$可以转化为对数式 $4={\log }_{2}16$，对数式 $2={\log }_{3}9$可以转化为指数式 $3^2=9$．

我们根据对数的定义可得到对数的一个性质：

${\log }_a(M\cdot N)={\log }_{a}M+{\log }_{a}N(a>0$， $a\ne 1$， $M>0$， $N>0)$，理由如下：

设 ${\log }_{a}M=m$， ${\log }_{a}N=n$，则 $M=a^m$， $N=a^n$，

$\therefore M\cdot N=a^m\cdot a^n=a^{m+n}$，由对数的定义得 $m+n={\log }_a(M\cdot N)$．

又 $\because m+n={\log }_{a}M+{\log }_{a}N$，

$\therefore {\log }_a(M\cdot N)={\log }_{a}M+{\log }_{a}N$．

根据上述材料，结合你所学的知识，解答下列问题：

（1）填空：① ${\log }_{2}32=$　　，② ${\log }_{3}27=$　　，③ ${\log }_{7}1=$　　；

（2）求证： ${\log }_a\frac{M}{N}={\log }_{a}M-{\log }_{a}N(a>0$， $a\ne 1$， $M>0$， $N>0)$；

（3）拓展运用：计算 ${\log }_{5}125+{\log }_{5}6-{\log }_{5}30$．

我们知道，任意一个正整数 $n$ 都可以进行这样的分解： $n=p\times q(p$ ， $q$ 是正整数，且 $p⩽q)$ ，在 $n$ 的所有这种分解中，如果 $p$ ， $q$ 两因数之差的绝对值最小，我们就称 $p\times q$ 是 $n$ 的最佳分解．并规定： $F\left(n\right)=\frac{p}{q}$ ．例如12可以分解成 $1\times 12$ ， $2\times 6$ 或 $3\times 4$ ，因为 $12-1>6-2>4-3$ ，所以 $3\times 4$ 是12的最佳分解，所以 $F\left(12\right)=\frac{3}{4}$ ．

（1）如果一个正整数 $a$ 是另外一个正整数 $b$ 的平方，我们称正整数 $a$ 是完全平方数．求证：对任意一个完全平方数 $m$ ，总有 $F\left(m\right)=1$ ；

（2）如果一个两位正整数 $t$ ， $t=10x+y(1⩽x⩽y⩽9$ ， $x$ ， $y$ 为自然数），交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18，那么我们称这个数 $t$ 为"吉祥数"，求所有"吉祥数"中 $F\left(t\right)$ 的最大值．

观察以下等式：

第1个等式： $\frac{1}{3}\times (1+\frac{2}{1})=2-\frac{1}{1}$，

第2个等式： $\frac{3}{4}\times (1+\frac{2}{2})=2-\frac{1}{2}$，

第3个等式： $\frac{5}{5}\times (1+\frac{2}{3})=2-\frac{1}{3}$，

第4个等式： $\frac{7}{6}\times (1+\frac{2}{4})=2-\frac{1}{4}$．

第5个等式： $\frac{9}{7}\times (1+\frac{2}{5})=2-\frac{1}{5}$．

$\dots$

按照以上规律，解决下列问题：

（1）写出第6个等式：　 $\frac{11}{8}\times (1+\frac{2}{6})=2-\frac{1}{6}$　；

（2）写出你猜想的第 $n$个等式：　　（用含 $n$的等式表示），并证明．

用※定义一种新运算：对于任意实数 $m$ 和 $n$ ，规定 $m$ ※ $n=m^{2}n-\mathit{mn}-3n$ ，如：1※ $2=1^2\times 2-1\times 2-3\times 2=-6$ ．

（1）求 $(-2)$ ※ $\sqrt{3}$ ；

（2）若3※ $m⩾-6$ ，求 $m$ 的取值范围，并在所给的数轴上表示出解集．

已知两个有理数： $-9$ 和5．

（1）计算： $\frac{(-9)+5}{2}$ ；

（2）若再添一个负整数 $m$ ，且 $-9$ ，5与 $m$ 这三个数的平均数仍小于 $m$ ，求 $m$ 的值．