某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
| 与标准质量的差值 (单位:g) |
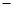 5 5 |
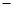 2 2 |
0 |
1 |
3 |
6 |
| 袋 数 |
1 |
4 |
3 |
4 |
5 |
3 |
(1)这批样品的平均质量比标准质量多还是少?多或少几克?
(2)若每袋标准质量为450克,则抽样检测的总质量是多少?
(1)计算: .
(2)下面是小明同学解不等式的过程,请认真阅读并完成相应任务.
.
解: 第一步
第二步
第三步
第四步
第五步
任务一:填空:①以上解题过程中,第二步是依据 (运算律)进行变形的;
②第 步开始出现错误,这一步错误的原因是 ;
任务二:请直接写出该不等式的正确解集.
炒股员小李上星期日买进某公司股票1000股,每股28元,下表为本周内该股票的涨跌情况(单位:元)
| 星期 |
一 |
二 |
三 |
四 |
五 |
六 |
| 每股涨跌 |
+4 |
-6 |
-1 |
-2.5 |
+4.5 |
+2 |
(1)星期四收盘时,每股是多少钱?
(2)本周内最高价和最低价各是多少钱?
(3)已知小李买进股票时付了1.5‰的手续费(a‰表示千分之a),卖出时需付成交额1.5‰的手续费和1‰的交易税,如果他在周六收盘前将全部股票卖出,他的收益情况如何?
我们常用“水滴石穿”来说明一个人只要持之以恒地做某件事,就一定能成功.经测算,当水滴不断地滴在一块石头上时,经过10年,石头上可形成一个深为1厘米的小洞,那么平均每个月小洞的深度增加多少米?(结果保留三个有效数字,并用科学记数法表示)
设a,b是任意两个实数,规定a与b之间的一种运算“⊕”为: ,
例如: ,
(因为 )
参照上面材料,解答下列问题:
(1) , ;
(2)若 ,且满足 ,求x的值.
计算:
(1)7÷(-  )×(
)×( -
-  );
);
(2)2a-3b+[4a-(3a-b)];
(3)(-x2)4+x3·x5-(3x4)2;
(4)(-  )-1+(-2)2×50;
)-1+(-2)2×50;
我们知道,任意一个正整数 都可以进行这样的分解: , 是正整数,且 ,在 的所有这种分解中,如果 , 两因数之差的绝对值最小,我们就称 是 的最佳分解.并规定: .例如12可以分解成 , 或 ,因为 ,所以 是12的最佳分解,所以 .
(1)如果一个正整数 是另外一个正整数 的平方,我们称正整数 是完全平方数.求证:对任意一个完全平方数 ,总有 ;
(2)如果一个两位正整数 , , , 为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18,那么我们称这个数 为"吉祥数",求所有"吉祥数"中 的最大值.
阅读以下材料:
苏格兰数学家纳皮尔 . , 年)是对数的创始人.他发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉 , 年)才发现指数与对数之间的联系.
对数的定义:一般地,若 且 ,那么 叫做以 为底 的对数,记作 ,比如指数式 可以转化为对数式 ,对数式 可以转化为指数式 .
我们根据对数的定义可得到对数的一个性质:
, , , ,理由如下:
设 , ,则 , ,
,由对数的定义得 .
又 ,
.
根据上述材料,结合你所学的知识,解答下列问题:
(1)填空:① ,② ,③ ;
(2)求证: , , , ;
(3)拓展运用:计算 .
观察以下等式:
第1个等式: ,
第2个等式: ,
第3个等式: ,
第4个等式: .
第5个等式: .
按照以上规律,解决下列问题:
(1)写出第6个等式: ;
(2)写出你猜想的第 个等式: (用含 的等式表示),并证明.
用※定义一种新运算:对于任意实数 和 ,规定 ※ ,如:1※ .
(1)求 ※ ;
(2)若3※ ,求 的取值范围,并在所给的数轴上表示出解集.
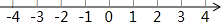
已知两个有理数: 和5.
(1)计算: ;
(2)若再添一个负整数 ,且 ,5与 这三个数的平均数仍小于 ,求 的值.