在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点.观察图中每一个正方形(实线)四条边上的整点的数.
(1)画出由里向外的第 个正方形,求在第四个正方形边上有多少个整点?
(2)请你猜测由里向外第 个正方形(实线)四条边上的整点共有多少个;
(3)探究点 在由里向外的第几个正方形的边上,点 在由里向外的第几个正方形的边上.

如图,将长方形 放置在平面直角坐标系中, 轴,且 ,且 .

(1)求 的坐标,并说明将长方形 进行怎样的平移使 点移到 点处;
(2) 轴上是否存在点 ,使 的面积等于长方形 面积的 ,若存在,求出 点坐标;若不存在,说明理由.
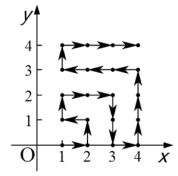
在平面直角坐标系中,一蚂蚁从原点 出发,按向上、向右、向下、向右方向依次不断移动,每次移动 个单位,其行走路线如图所示.
(1)填写下列各点的坐标:
( ), ( ), ( )
(2)写出点 的坐标( 是正整数);
(3)指出蚂蚁从点 到点 的移动方向.

如图所示, 是由 平移后得到的,已知 中任意一点 经平移后对应点为 .
(1)已知 ,请写出 的坐标
(2)试说明 是如何由 得到的?
(3)连接 ,求出五边形 的面积.

在一单位 的方格纸上, …,斜边都在 轴上,斜边长分别为 的等腰直角三角形.若 的顶点坐标分别为 ,则依图中所示规律, 的坐标为_____.
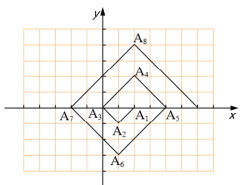
如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如 ,按这个规律,第 个点的坐标为_____.
圆心在 轴上的两圆相交于 两点,已知 点的坐标为 ,则 点的坐标为_____.
如图,平面中两条直线 和 相交于点 ,对于平面上任意一点 ,若 分别是 到直线 和 的距离,则称有序非负数对 是点 的“距离坐标”.根据上述定义,有以下几个结论:
①“距离坐标”是 的点有 个;
②“距离坐标”是 的点有 个;
③“距离坐标”是 ( 为非负实数)的点有 个.
其中正确的个数有( )

| A. | 个 |
B. | 个 |
C. | 个 |
D. | 个 |
如图,一个粒子在第一象限内及 轴上运动,在第一分钟内它从原点运动到 ,而后它接着按图中所示在与 轴, 轴平行的方向上来回运动,且每分钟移动 个长度单位,那么,在 后这个粒子所处的位置是( )

| A. |
|
B. |
|
C. |
|
D. |
|
在直角坐标系中,我们把横、纵坐标都为整数的点叫做整点,且规定正方形的内部不包含边界上的点.观察图中所示的中心在原点,一边平行于 轴的正方形:边长为 的正方形内部有 个整点,边长为 的正方形内部有 个整点,边长为 的正方形内部有 个整点,…,则边长为 的正方形内部的整点的个数为( )

| A. |
|
B. |
|
C. |
|
D. |
|
第二象限有一点 ,且 ,则点 关于原点的对称点的坐标是( )
| A. |
|
B. |
|
C. |
|
D. |
|