如图所示，有一半径为R的半球形凹槽P，放在光滑的水平地面上，一面紧靠在光滑墙壁上，在槽口上有一质量为m的小球，由A点静止释放，沿光滑的球面滑下，经最低点B又沿球面上升到最高点C，经历的时间为t，B、C两点高度差为0.6R，求：
(1)小球到达C点的速度。
(2)在t这段时间里，竖墙对凹槽的冲量
如图所示，在光滑的水平面上放置一质量为m的小车，小车上有一半径为R的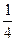
光滑的弧形轨道，设有一质量为m的小球，以v0的速度，方向水平向左沿圆弧轨道向上滑动，达到某一高度h后，又沿轨道下滑，试求h的大小及小球刚离开轨道时的速度．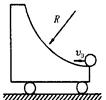
如图所示，在光滑的水平杆上套者一个质量为m的滑环，滑环上通过一根不可伸缩的轻绳悬吊着质量为M的物体（可视为质点），绳长为L。将滑环固定时，给物块一个水平冲量，物块摆起后刚好碰到水平杆，若滑环不固定，仍给物块以同样的水平冲量，求物块摆起的最大高度。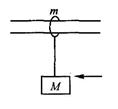
如图所示，质量为m的有孔物体A套在光滑的水平杆上，在A下面用细绳挂一质量为M的物体B，若A固定不动，给B一水平冲量I，B恰能上升到使绳水平的位置。当A不固定时，要使B物体上升到使绳水平的位置，则给它的水平冲量至少多大?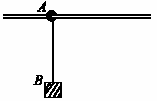
一个质量为M，底面边长为b的三角形劈块静止于光滑水平面上，如图，有一质量为m的小球由斜面顶部无初速滑到底部的过程中，劈块移动的距离是多少？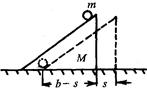
人和冰车的总质量为M，另有一个质量为m的坚固木箱，开始时人坐在冰车上静止在光滑水平冰面上，某一时刻人将原来静止在冰面上的木箱以速度V推向前方弹性挡板，木箱与档板碰撞后又反向弹回，设木箱与挡板碰撞过程中没有机械能的损失，人接到木箱后又以速度V推向挡板，如此反复多次，试求人推多少次木箱后将不可能再接到木箱？（已知
）
如图所示为三块质量均为m，长度均为L的木块。木块1和木块2重叠放置在光滑的水平桌面上，木块3沿光滑水平桌面运动并与叠放在下面的木块2发生碰撞后粘合在一起，如果要求碰后原来叠放在上面的木块1完全移到木块3上，并且不会从木块3上掉下，木块3碰撞前的动能应满足什么条件？设木块之间的动摩擦因数为m。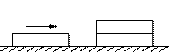
如图所示，一质量为M、长为L的长方形木板B放在光滑的水平地面上，在其右端放一质量为m的小木块A，m＜M。现以地面为参照系，给A和B以大小相等、方向相反的初速度(如图1)，使A开始向左运动，B开始向右运动，但最后A刚好没有滑离B板，以地面为参照系。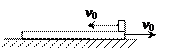
(1)若已知A和B的初速度大小为V0，求它们最后的速度大小和方向。
(2)若初速度的大小未知，求小木块A向左运动到达的最远处(从地面上看)离出发点的距离。
蹦床是运动员在一张绷紧的弹性网上蹦跳、翻滚并做各种空中动作的运动项目。一个质量为60kg的运动员，从离水平网面3.2m高处自由下落，着网后沿竖直方向蹦回离水平网面5.0m高处。已知运动员与网接触的时间为1.2s。若把在这段时间内网对运动员的作用力当作恒力处理，求此力的大小。（g取10m/s2）
如图所示，以Vo ＝10m／s2的初速度、与水平方向成300角抛出一个质量m＝2kg的小球．忽略空气阻力的作用，g取10m／s2．求抛出后第2s末小球速度的大小．
某种气体分子束由质量m=5.4X10-26kg速度V＝460m/s的分子组成，各分子都向同一方向运动，垂直地打在某平面上后又以原速率反向弹回，如分子束中每立方米的体积内有n0＝1.5X1020个分子，求被分子束撞击的平面所受到的压强．
总质量为M的列车以匀速率v0在平直轨道上行驶，各车厢受的阻力都是车重的k倍，而与车速无关。某时刻列车后部质量为m的车厢脱钩，而机车的牵引力不变，则脱钩的车厢刚停下的瞬间，前面列车的速度是多少？
如图所示，在光滑的水平面上静止着一个质量为m2小球2，质量为m1的小球1以一定的初速度v1朝着球2运动，如果两球之间、球与墙之间发生的碰撞均无机械能损失，要使两球还能再碰，则两小球的质量需满足怎样的关系？
粤公网安备 44130202000953号