高中物理综合题

如图所示，光滑斜面的倾角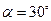，在斜面上放置一矩形线框abcd，ab边的边长为1 m，bc边的边长为0. 8 m ，线框的质量M="4" kg，电阻为0. 1Ω，线框通过细线绕过光滑的定滑轮与重物相连，滑轮的质量不计，重物的质量m="1" kg，斜面上ef和gh为斜面上有界匀强磁场的边界，与斜面的底边平行，ef和gh的间距为1. 8 m，磁场方向垂直于斜面向上，B="0." 5 T，开始cd边离gh边的距离为2.25 m，由静止释放，线框恰好能匀速穿过ef边界，线框滑动过程中cd边始终与底边平行，求：（设斜面足够长，重物m不会与滑轮接触，g取10 ）
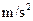（1）线框cd边刚进入磁场时速度的大小。
（2）线框进入磁场过程中通过线框的电量。
（3）线框进入磁场过程中在线框中产生的焦耳热。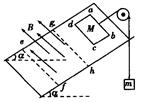

如图所示，两平行的光滑金属导轨相距为L，且位于同一竖直平面内，两导轨间接有电阻R，轻质金属杆ab长为2L，紧贴导轨竖直放置，距b端为L/2处固定有质量为m的球。整个装置处于磁感应强度为B并垂直于导轨平面的匀强磁场中，当ab杆由静止开始紧贴导轨绕b端向右自由倒下至水平位置时，球的速度为v，若导轨足够长，导轨及金属杆电阻不计，试求此过程中：
（1）电阻R消耗的电能；
（2）R中的电流最大值。

如图所示，无动力传送带水平放置，传送带的质量M＝5kg，长L＝5m，轮与轴间的摩擦及轮的质量均不计．质量为m=2kg的工件从光滑弧面上高为h=0.45m的a点由静止开始下滑，到b点又滑上静止的传送带，工件与皮带之间的动摩擦因数，求：
⑴工件离开传送带时的速度；
⑵工件在传送带上运动的时间；
⑶系统损失的机械能．

如图所示，要在客厅里挂一幅质量m=1.2kg的画（含画框），已知画框背面有两个相距l=0.8m、位置固定的挂钩。现将轻质细绳的两端分别固定在两个挂钩上，把画对称地挂在插入竖直墙壁的光滑钉子上，挂好后整条细绳呈绷紧状态。若细绳能够承受的最大拉力为F_max=10N，g取10m/s²，要使细绳不被拉断，求细绳的最小长度。

 

 

如图所示，两个完全相同的小球，重力大小为G，两球与水平面的动摩擦因数都为μ，一根轻绳两端固定在两小球上，在绳的中点施加一个竖直向上的拉力，当绳子被拉直后，两段绳的夹角为α，问当F至少为多大，两球将会发生滑动？（假设最大静摩擦等于滑动摩擦力）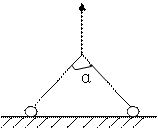

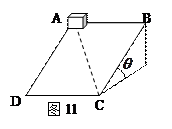
如图11所示，矩形斜面ABCD倾角θ=37°，AD=BC=2m,AB=DC=1.5m,有一小立方体铁块P(可当作质点)质量为2kg,能够静止在斜面上,现对小铁块P施加一个向右的平行于AB的拉力T, 小铁块恰好沿对角线AC匀速下滑,求:
拉力T的大小,
小铁块P与斜面间的动摩擦因数,

）重量为G₁的均匀球夹在光滑竖直平面和45°倾角的光滑斜块之间，如图所示，斜块重G₂，斜块侧面与水平桌面间的摩擦系数为m₀，求：G₁的最小值为多大时，才能使斜块滑动。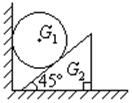

一瓶有放射性同位素的溶液，测得平均每分钟内有8×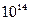个 原 子 发 生 衰 变。已 知 该 同 位 素的 半 衰 期 为 2天，衰 变 后 的 物 质 不 具 有 放 射 性。现 将 该 溶 液 倒 入 水 库， 设 10天 后 溶 液 均匀分布到库水中，这时从水库中取出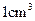的水，测得平均每分钟内有20个原子发生衰变，能否由此推算该水库中现存的水量？

氢原子处于基态时，原子的能量为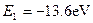，问：
（1）氢原子在n =4的定态时，可放出几种频率的光？其中最小频率等于多少Hz？
（2）若要使处于基态的氢原子电离，至少要用多大频率的电磁波照射此原子？

假设两个氘核在同一直线上相碰发生聚变反应生成氦同位素和中子，已知氘核的质量为2.0136u，中子的质量为1.0087u，氦的同位素的质量为3.0150u，求该聚变反应中释放的能量（保留两位有效数字）。

四个质子在高温下能聚变成一个α粒子，同时释放能量，已知质子的质量为1.007276 u，α粒子的质量为4.001506 u，阿伏加德罗常数为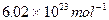，求10g氢完全聚变成α粒子所释放的能量。

两个氘核聚变产生一个中子和一个氦核（氦的同位素），若在反应前两个氘核的动能均为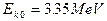，它们正面碰撞发生核聚变，且反应后释放的能量全部转化为动能，反应后所产生的中子的动能为2.49MeV，求该核反应所释放的核能。已知氘核的质量为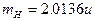，氦核的质量为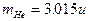，中子的质量为。

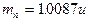两个动能均为1Mev的氘核发生正面碰撞，引起了如下的核反应: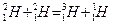试求:
①此核反应中放出的能量ΔΕ 等于多少?
②若放出的能量全部变成核的动能，则生成的氢核具有的动能是多少?（已知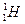、、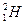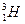的原子核的质量分别为1.0073u、2.0136u 、3.0156u）

—束光由真空射到平面玻璃上，当其折射角为30º时，反射光恰好产生完全偏振，试求玻璃的折射率．

一种红宝石激光器发射的激光是不连续的一道道闪光，每道闪光称为—个光脉冲．若这种激光器光脉冲的持续时间为1.0×10-11，波长为694。3nm，发射功率为1.0×lO10W，问(1)每列光脉冲的长度是多少?(2)用红宝石激光器照射皮肤上色斑，每l0mm2色斑上吸收能量达到60J以后，便逐渐消失．一颗色斑的面积为50mm2，则要吸收多少个红宝石激光脉冲，才能逐渐消失?