不等式ex-x>ax的解集为P,且[0,2]⊆P,则实数a的取值范围是( )
| A.(-∞,e-1) | B.(e-1,+∞) | C.(-∞,e+1) | D.(e+1,+∞) |
已知命题p:函数y=log0.5(x2+2x+a)的值域为R.命题q:函数y=-(5-2a)x是R上的减函数.若p或q为真命题,p且q为假命题,则实数a的取值范围是________.
已知函数f(x)=1-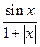 (x∈R)的最大值为M,最小值为m,则M+m=_.
(x∈R)的最大值为M,最小值为m,则M+m=_.
已知函数f(x)=lnx+2x,g(x)=a(x2+x),若f(x)≤g(x)恒成立,则实数a的取值范围是________.
(12分)已知命题p:方程a2x2+ax-2=0在[-1,1]上有且仅有一解.命题q:只有一个实数x满足不等式x2+2ax+2a≤0.若命题“p或q”是假命题,求a的取值范围.
(12分)如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.
(1)分别求出函数f(x)和g(x)的解析式;
(2)如果函数y=g(f(x))在区间[1,m)上单调递减,求m的取值范围.
(13分)已知函数f(x)=ax2+2x+c(a、c∈N*)满足:
①f(1)=5;②6<f(2)<11.
(1)求a、c的值;
(2)若对任意的实数x∈ ,都有f(x)-2mx≤1成立,求实数m的取值范围.
,都有f(x)-2mx≤1成立,求实数m的取值范围.
(14分)设函数f(x)=ax2+bx+k(k>0)在x=0处取得极值,且曲线y=f(x)在点(1,f(1))处的切线垂直于直线x+2y+1=0.
(1)求a,b的值;
(2)若函数g(x)= ,讨论g(x)的单调性.
,讨论g(x)的单调性.
(12分)(2010·山东德州模拟)已知f(x)=(x2+ax+a)e-x(a≤2,x∈R).
(1)当a=1时,求f(x)的单调区间;(2)若f(x)的极大值为4e-2,求出a的值.
设 与
与 是定义在同一区间
是定义在同一区间 上的两个函数,若对任意的
上的两个函数,若对任意的 ,
,
都有 ,则称
,则称 和
和 在
在 上是“密切函数”,
上是“密切函数”, 称为“密切区
称为“密切区
间”,设 与
与 在
在 上
上 是“密切函数”,则它的“密切区间”
是“密切函数”,则它的“密切区间”
可以是 ( )
A. |
B. |
C.  |
D. |