高中数学试题

计算＝              

(本小题满分12分)
已知数列是等差数列，；数列的前n项和是，且．
(Ⅰ) 求数列的通项公式；
(Ⅱ) 求证：数列是等比数列；
(Ⅲ) 记，求的前n项和．

，，的大小关系为

A．	B．
C．	D．

已知函数（其中）的图象如下面右图所示，则函数的图象是

已知全集     

计算：
（1)
（2）

已知指数函数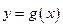满足：g(3)=8，定义域为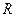的函数是奇函数.
（1）确定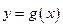的解析式；
（2）求m，n的值；
（3）若对任意的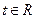，不等式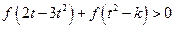恒成立，求实数的取值范围

等差数列｛｝的公差不为零，首项＝1，是和的等比中项，则数列的前10项之和是

A．90

B．100

C．145

D．190

在中，角A、B、C所对应的边分别为a、b、c，若角A、B、C依次成等差数列，且a=1，等于
A．             B．           C．           D．2

已知x、y满足约束条件则目标函数z＝(x＋1)²＋(y－1)²的最大值是

A．10

B．90

C．

D．2

设等比数列的公比，前项和为，则      

运货卡车以每小时x千米的速度匀速行驶130千米(50≤x≤100)(单位：千米/小时)．假设汽油的价格是每升2元，而汽车每小时耗油(2＋)升，司机的工资是每小时14元
(Ⅰ)求这次行车总费用y关于x的表达式
(Ⅱ)当x为何值时，这次行车的总费用最低，并求出最低费用的值

某人5次上班途中所花的时间(单位：分钟)分别为8，12，10，11，9．若这组数据的平均数为x，方差为y，则|x－y|的值为(　　)

A．0

B．2

C．4

D．8

已知某个几何体的三视图如下，根据图中标出的尺寸（单位：cm），可

得这个几何体的体积是(　   )
A．      B．
C．       D．

已知正项等比数列{}满足：，若存在两项、，使得，则 的最小值为(　　)

A．

B．

C．

D．不存在